Trang chủ
Đề thi & kiểm tra
Toán học
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
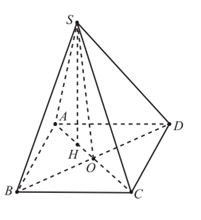
Cho hình chóp S.ABCD có SC=x( 0
Cho hình chóp S.ABCD có SC=x( 0
Câu hỏi :
Cho hình chóp S.ABCD có các cạnh còn lại đều bằng a. Biết rằng thể tích khối chóp S.ABCD lớn nhất khi và chỉ khi . Mệnh đề nào sau đây đúng?
Cho hình chóp S.ABCD có các cạnh còn lại đều bằng a. Biết rằng thể tích khối chóp S.ABCD lớn nhất khi và chỉ khi . Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
* Đáp án
A
* Hướng dẫn giải
Đáp án A
|
Vì nên hình chiếu vuông góc của S trên (ABCD) trùng với tâm đường tròn ngoại tiếp tam giác ABD. Gọi H là tâm đường tròn ngoại tiếp tam giác
Do tam giác ABD cân tại Dễ dàng chứng minh được: vuông tại S (tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh ấy) |
|
Áp dụng hệ thức lượng trong tam giác vuông SAC có
Ta có
Do ABCD là hình thoi
Khi đó ta có:
Áp dụng BĐT Cosi ta có:
Dấu “=” xảy raCâu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Số câu hỏi: 1250
Copyright © 2021 HOCTAP247
