Trang chủ
Đề thi & kiểm tra
Toán học
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Cho hình chóp có đáy S. ABCD là hình bình...
Cho hình chóp có đáy S. ABCD là hình bình hành. Gọi M là điểm đối xứng của C qua B và là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S. ABCD thành hai khối đa diện, trong đó...
Câu hỏi :
Cho hình chóp có đáy S. ABCD là hình bình hành. Gọi M là điểm đối xứng của C qua B và là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S. ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ dưới đây). Tính tỉ số .
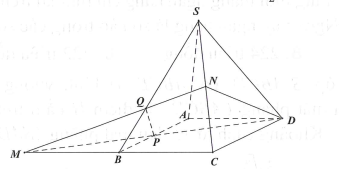

A. .
B.
C.
D.
* Đáp án
D
* Hướng dẫn giải
Đáp án D
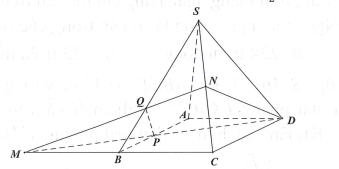
Gọi V là thể tích khối chóp .
Có là trung điểm của AB.
Ta có
Mà
Xét tam giác , áp dụng định lý Mênêlauýt cho bộ ba điểm thẳng hàng ta có:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT Quốc gia môn Toán có chọn lọc và lời giải chi tiết (25 đề) !!
Số câu hỏi: 1250
Copyright © 2021 HOCTAP247
