Trong không gian Oxyz, cho tứ diện ABCD có tọa độ các điểm A(1;1;1) ,B(2;0;2) ,C(-1;-1;0) , D(0;3;4) . Trên các cạnh AB, AC, AD lần lượt lấy các điểm B', C' , D' sao cho AB/AB'+AC/...

Đáp án D

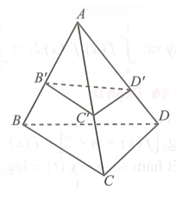
Ta có $\frac{V_{ABCD}}{V_{A{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}}}=\frac{AB}{A{B}^{\text{'}}}.\frac{AC}{A{C}^{\text{'}}}.\frac{AD}{A{D}^{\text{'}}}\le {\left(\frac{\frac{AB}{A{B}^{\text{'}}}+\frac{AC}{A{C}^{\text{'}}}+\frac{AD}{A{D}^{\text{'}}}}{3}\right)}^3={\left(\frac{4}{3}\right)}^3$  .

Do đó thể tích của  nhỏ nhất khi và chỉ khi $\frac{AB}{A{B}^{\text{'}}}=\frac{AC}{A{C}^{\text{'}}}=\frac{AD}{A{D}^{\text{'}}}=\frac{4}{3}$ .

Khi đó $\overrightarrow{A{B}^{\text{'}}}=\frac{3}{4}\overrightarrow{AB}\Rightarrow B^{\text{'}}(\frac{7}{4};\frac{1}{4};\frac{7}{4})$   và $\left(B^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}\right)\text{//}\left(BCD\right)$ .

Mặt khác $[\overrightarrow{BC},\overrightarrow{BD}]=(4;10;-11)$ .

Vậy $\left(B^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}\right):4(x-\frac{7}{4})+10(y-\frac{1}{4})-11(z-\frac{7}{4})=0\iff 16x+40y-44z+39=0$ .