Trong không gian với hệ tọa độ Oxyz, cho ba điểm P, Q, R lần lượt di động trên ba trục tọa độ Ox, Oy, Oz (không trùng với gốc tọa độ O) sao cho 1/OP^2+z/OQ^2+z/OR^2=1/8 . Biết mặt...

Đáp án D

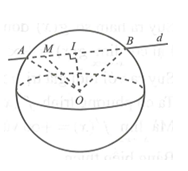
Gọi H là hình chiếu vuông góc của điểm O trên mặt phẳng $\left(PQR\right)$ .

Dễ thấy $\frac{1}{O{H}^2}=\frac{1}{O{P}^2}+\frac{1}{O{Q}^2}+\frac{1}{O{R}^2}$   hay $\frac{1}{O{H}^2}=\frac{1}{8}$  hay $OH=2\sqrt{2}$ .

Khi đó suy ra mặt phẳng $\left(PQR\right)$  luôn tiếp xúc với mặt cầu (S) tâm O, bán kính $R=2\sqrt{2}$ .

Ta có $OM=\sqrt{\frac{1}{4}+\frac{3}{4}+0}=1<R$  nên điểm M nằm trong mặt cầu (S).

Gọi I là trung điểm của AB, do tam giác OAB cân tại O nên $S_{\Delta OAB}=\frac{1}{2}OI.AB$ .

Đặt $OI=x$ , vì  $OI\le OM$ nên $0<x\le 1$   và $AB=2\sqrt{8-x^2}$ .

Ta có $S_{\Delta OAB}=\frac{1}{2}x.2\sqrt{8-x^2}=x\sqrt{8-x^2}=\sqrt{8x^2-x^4}$  .

Xét hàm số $f\left(x\right)=8x^2-x^4$  với $0<x\le 1$ .

Có $f^{\text{'}}\left(x\right)=16x-4x^3=4x(4-x^2)>0$ , $x\in (0;1]$

$\Rightarrow f\left(x\right)\le f\left(1\right)=7$.

Suy ra diện tích của tam giác OAB lớn nhất bằng $\sqrt{7}$  đạt được khi M là trung điểm của AB.