Trong không gian Oxyz, cho hai điểm A(0;0;2), B( 1;1;0) và mặt cầu (S): x^2+y^2+(z-1)^2=1/4 . Xét điểm M thay đổi thuộc (S) . Giá trị nhỏ nhất của biểu thức MA^2+2MB^2 bằng:

Đáp án D

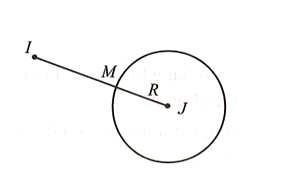
Gọi $I(a;b;c)$  là điểm thỏa mãn $\overrightarrow{IA}+2\overrightarrow{IB}=\overrightarrow{0}$

Ta có $\{\begin{array}{l}-a+2-2\text{a}=0\\ -b+2-2b=0\\ 2-c-2c=0\end{array}\iff \{\begin{array}{l}a=\frac{2}{3}\\ b=\frac{2}{3}\\ c=\frac{2}{3}\end{array}\Rightarrow I(\frac{2}{3};\frac{2}{3};\frac{2}{3})$

Ta có:  $M{A}^2+2M{B}^2={(\overrightarrow{MI}+\overrightarrow{IA})}^2+2{(\overrightarrow{MI}+\overrightarrow{IB})}^2$

 $=M{I}^2+2\overrightarrow{MI}.\overrightarrow{MA}+I{A}^2+2M{I}^2+4\overrightarrow{MI}.\overrightarrow{IB}+I{B}^2$

$=3M{I}^2+I{A}^2+2I{B}^2+2\overrightarrow{MI}\underset{0}{\underbrace{(\overrightarrow{IA}+2\overrightarrow{IB})}}=3M{I}^2+\underset{const}{\underbrace{I{A}^2+2I{B}^2}}=3M{I}^2+I{A}^2+2I{B}^2+2\overrightarrow{MI}\underset{0}{\underbrace{(\overrightarrow{IA}+2\overrightarrow{IB})}}=3M{I}^2+\underset{const}{\underbrace{I{A}^2+2I{B}^2}}$

Do $\{\begin{array}{l}I{A}^2={(-\frac{2}{3})}^2+{(-\frac{2}{3})}^2+{(2-\frac{2}{3})}^2=\frac{8}{3}\\ I{B}^2={(1-\frac{2}{3})}^2+{(1-\frac{2}{3})}^2+{(-\frac{2}{3})}^2=\frac{2}{3}\end{array}\Rightarrow I{A}^2+2I{B}^2=4$   không đổi, nên ${(M{A}^2+2M{B}^2)}_{\min }\iff M{I}_{\min }$

 với $I(\frac{2}{3};\frac{2}{3};\frac{2}{3}),\text{ M}\in \left(S\right)$ .

Ta có  ${\left(\frac{2}{3}\right)}^2+{\left(\frac{2}{3}\right)}^2+{(\frac{2}{3}-1)}^2=1>\frac{1}{4}\Rightarrow I$nằm ngoài  (S)

Khi đó $M{I}_{\min }=IJ-R$  với  $J(0;0;1)$là tâm mặt cầu, $R=\frac{1}{2}$  là bán kính mặt cầu.

Ta có: $\text{IJ}=\sqrt{{(-\frac{2}{3})}^2+{(-\frac{2}{3})}^2+{(1-\frac{2}{3})}^2}=1\Rightarrow M{I}_{\min }=1-\frac{1}{2}=\frac{1}{2}$

Vậy ${(M{A}^2+2M{B}^2)}_{\min }=3M{I}_{\min }^2+4=3.{\left(\frac{1}{2}\right)}^2+4=\frac{19}{4}$ .