Cho khối chóp S.ABC có SA=SB=SC=a, góc ASB=60 độ, góc BSC= 90 độ, Góc ASC=120 độ. Gọi M, N lần lượt là các điểm trên cạnh AB và SC sao cho CN/SC=AM/AB . Khi khoảng cách giữa M và N...

Đáp án C

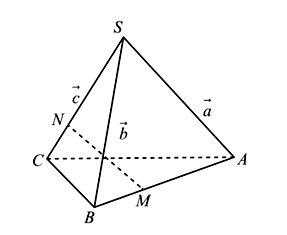
Ta có thể tích khối chóp S.ABC là

$V_0=\frac{a^3}{6}\sqrt{1-{\left(\frac{1}{2}\right)}^2-{(-\frac{1}{2})}^2}=\frac{\sqrt{2}{a}^3}{12}$.

Đặt  $\frac{CN}{SC}=\frac{AM}{AB}=m$  (với $0\le m\le 1$ ).

Ta có: $\overrightarrow{SA}=\overrightarrow{a},\overrightarrow{SB}=\overrightarrow{b},\overrightarrow{SC}=\overrightarrow{c},\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=\left|\overrightarrow{c}\right|=a$  ,

$\overrightarrow{a}.\overrightarrow{b}=\frac{a^2}{2},\overrightarrow{b}.\overrightarrow{c}=\mathrm{0,}\overrightarrow{a}.\overrightarrow{c}=-\frac{a^2}{2}$.

Theo đẳng thức trên ta có đẳng thức véctơ $\overrightarrow{SN}=(1-m)\overrightarrow{c}$  , $\overrightarrow{SM}=\overrightarrow{SA}+\overrightarrow{AM}=\overrightarrow{a}+m\overrightarrow{AB}=\overrightarrow{a}+m(\overrightarrow{b}-\overrightarrow{a})$

$\Rightarrow \overrightarrow{MN}=\overrightarrow{SN}-\overrightarrow{SM}=(1-m)\overrightarrow{c}-[\overrightarrow{a}+m(\overrightarrow{b}-\overrightarrow{a})]=(m-1)\overrightarrow{a}-m\overrightarrow{b}+(1-m)\overrightarrow{c}$.

Do đó $M{N}^2={[(m-1)\overrightarrow{a}-m\overrightarrow{b}+(1-m)\overrightarrow{c}]}^2=(3m^2-5m+3)a^2\ge \frac{11{\text{a}}^2}{12}$ .

Dấu “=” xảy ra tại $m=\frac{5}{6}$

$\Rightarrow V=\frac{SN}{SC}.V_{S.ABC}=\frac{SN}{SC}.\frac{AM}{AB}{V}_0=m(1-m)V_0=\frac{5}{6}.\frac{1}{6}.\frac{\sqrt{2}{a}^3}{12}=\frac{5\sqrt{2}{a}^3}{432}$.