Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC) là một điểm nằm trên đoạn thẳng BC. Mặt phẳng (SAB) tạo với (SBC) m...

Đáp án C

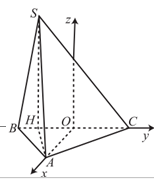
Gọi O là trung điểm của BC, qua O kẻ tia Oz cắt SC tại B.

Gắn hệ trục tọa độ như hình vẽ, ở đó:

  $O(0;0;0),A(1;0;0),B(0;-1;0),C(0;1;0),S(0;m;n)$.

$\Rightarrow \overrightarrow{AB}=(-1;-1;0),\overrightarrow{AC}=(-1;1;0),\overrightarrow{AS}=(-1;m;n)$.

Mặt phẳng $\left(SBC\right):x=0$  có vectơ pháp tuyến $\overrightarrow{i}=(1;0;0)$ .

Mặt phẳng $\left(SAC\right)$  có vectơ pháp tuyến $\overrightarrow{n_1}=[\overrightarrow{AC},\overrightarrow{AS}]=(n;n;-m+1).$

Mặt phẳng $\left(SAB\right)$   có vectơ pháp tuyến $\overrightarrow{n_2}=[\overrightarrow{AB},\overrightarrow{AS}]=(-n;n;-m-1).$

$\begin{array}{l}\cos 60°=\frac{|\overrightarrow{n_1}.\overrightarrow{i}|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{i}\right|}=\frac{|-n|}{\sqrt{2n^2+{(-m-1)}^2}}\iff \frac{1}{2}=\frac{|-n|}{\sqrt{2n^2+{(-m-1)}^2}}\iff 4n^2=2n^2+{(-m-1)}^2\iff 2n^2={(-m-1)}^2\left(1\right)\\ \cos \phi =\frac{|\overrightarrow{n_1}.\overrightarrow{i}|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{i}\right|}=\frac{\left|n\right|}{\sqrt{2n^2+{(-m+1)}^2}}=\frac{\sqrt{2}}{4}\iff 4\left|n\right|=\sqrt{4n^2+2{(-m+1)}^2}\iff 6n^2={(1-m)}^2\left(2\right)\end{array}$Từ (1) và (2) suy ra  $3{(m+1)}^2={(1-m)}^2\iff [\begin{array}{l}m=-2+\sqrt{3}\\ m=-2-\sqrt{3}\end{array}\Rightarrow [\begin{array}{l}n=\sqrt{2-\sqrt{3}}\\ n=\sqrt{2+\sqrt{3}}\end{array}$ .

$\Rightarrow [\begin{array}{l}S(0;-2+\sqrt{3};\sqrt{2-\sqrt{3}})\\ S(0;-2-\sqrt{3};\sqrt{2+\sqrt{3}})\end{array}$

$\begin{array}{l}\Rightarrow [\begin{array}{l}H(0;-2+\sqrt{3};0)\\ H(0;-2-\sqrt{3};0)\end{array}\Rightarrow [\begin{array}{l}SH=\sqrt{2-\sqrt{3}},AH=\sqrt{1+{(-2+\sqrt{3})}^2}=2\sqrt{2-\sqrt{3}}\\ SH=\sqrt{2+\sqrt{3}},AH=\sqrt{1+{(-2-\sqrt{3})}^2}=2\sqrt{2+\sqrt{3}}\end{array}\\ \Rightarrow \tan \alpha =\frac{SH}{AH}=\frac{1}{2}\end{array}$