Cho tứ diện ABCD có AD vuông góc (ABCD) có tam giác vuông tại B. Biết BC=2x, AB=2a căn3, AD=6a . Quay tam giác ABC và AB (bao gồm cả điểm bên trong 2 tam giác) xung quanh đường thẳ...

Đáp án B

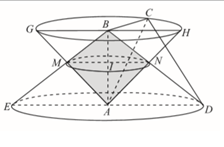
Trong mặt phẳng đáy của hình nón (N1)   kẻ đường kính GH//DE. Dễ dàng chứng minh được DEGH là hình thang cân.

Gọi $M=AG\cap BE;N=AH\cap BD;I=AB\cap MN$

Khi đó phần chung giữa hai khối nón (N1)  và (N2) là hai khối nón:

Khối nón (N3) đỉnh B, đường cao BI, bán kính đáy $IN\Rightarrow V_3=\frac{1}{3}\pi .I{N}^2.BI$

Khối nón (N4) đỉnh A, đường cao AI, bán kính đáy $IN\Rightarrow V_4=\frac{1}{3}\pi .I{N}^2.AI$

Thể tích phần chung $V=V_3+V_4=\frac{1}{3}\pi .I{N}^2.BI+\frac{1}{3}\pi .I{N}^2.AI=\frac{1}{3}\pi .I{N}^2.(AI+BI)=\frac{1}{3}\pi .I{N}^2.AB$

Áp dụng định lí Ta-let ta có: $\frac{MN}{GH}=\frac{AI}{AB};\frac{MN}{DE}=\frac{BI}{AB}\Rightarrow \frac{MN}{GH}+\frac{MN}{DE}=\frac{AI+BI}{AB}=1$

$\Rightarrow MN(\frac{1}{2BC}+\frac{1}{2AD})=1\iff MN.(\frac{1}{2.2a}+\frac{1}{2.6a})=1\iff MN=3a$

Dễ thấy I là trung điểm của $MN\Rightarrow IN=\frac{MN}{2}=\frac{3a}{2}$

Vậy $V=\frac{1}{3}\pi .{\left(\frac{3a}{2}\right)}^2.2a\sqrt{3}=\frac{3\sqrt{3}\pi a^3}{2}$