Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S)

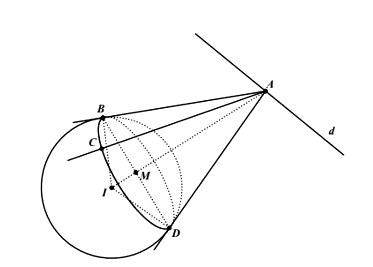
Gọi M là tâm đường tròn ngoại tiếp tam giác BCD

Trong các tam giác nội tiếp đường tròn thì tam giác đều có diện tích lớn nhất, vì vậy thể tích khối chóp I.BCD đạt giá trị lớn nhất khi thể tích khối nón đỉnh I đáy là đường tròn (I, IM) lớn nhất.

Gọi $IM=x,\left(0<x<\sqrt{3}\right)$ ta có thể tích khối nón $V=\frac{1}{3}IM.\pi .M{B}^2=\frac{\pi }{3}.x.\left(3-x^2\right).$

V đạt giá trị lớn nhất khi x = 1

Xét tam giác ABI vuông tại B, có đường cao BM tính được $IA=\frac{I{B}^2}{IM}=3,AB=\sqrt{6}.$

Gọi $A\left(1+2t;-6+3t;-2+2t\right)\in d,IA=3\iff {\left(2t-2\right)}^2+{\left(3t-8\right)}^2+{\left(2t-3\right)}^2=9\iff t=2.$

Tọa độ điểm A(5; 0; 2). Phương trình mặt cầu tâm A bán kính AB là:

$\left(S_1\right):{\left(x-5\right)}^2+y^2+{\left(z-2\right)}^2=6.$ Mặt phẳng (BCD) chứa giao tuyến của (S) và $\left(S_1\right)$ có phương trình thỏa mãn hệ: $\left\{\begin{array}{l}{\left(x-3\right)}^2+{\left(y-2\right)}^2+{\left(z-1\right)}^2=3\\ {\left(x-5\right)}^2+y^2+{\left(z-2\right)}^2=6\end{array}\right.\Rightarrow -4x+4y-2z+12=0.$

Đồng nhất với mặt phẳng $mx+ny+pz+12=0$ ta có m + n + p = -2.

Chọn C.