Cho lăng trụ tam giác ABC.A'B'C'. M, N lần lượt là trung điểm AB, AC; P

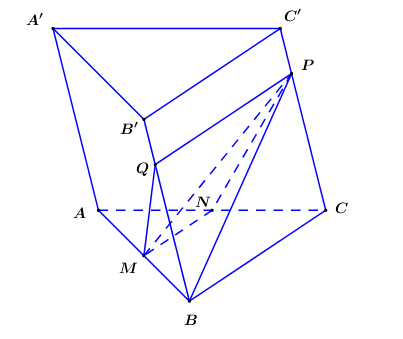
Xác định thiết diện của hình chóp cắt bởi (MNP)

Xét (MNP) và (BCC'B') có P chung, MN//BC (MN là đường trung bình của tam giác ABC)

$\Rightarrow \left(MNP\right)\cap \left(BCC\text{'}B\text{'}\right)=PQ//MN//BC\left(Q\in BB\text{'}\right).$

$\Rightarrow$ Thiết diện của hình chóp cắt bởi () là MNPQ.

Tính tỉ số thể tích

Khi đó mặt phẳng (MNP) chia hình lăng trụ thành 2 khối đa diện $BCMNPQ$ và $MNPQAA\text{'}B\text{'}C\text{'}.$

Đặt $V_{ABC.A\text{'}B\text{'}C\text{'}}=V,V_{BCMNPQ}=V_1,V_{MNPQAA\text{'}B\text{'}C\text{'}}=V_2.$

Theo bài ra ta có $\frac{V_1}{V_2}=\frac{1}{2}\Rightarrow V_1=\frac{1}{3}V.$

Ta có: $V_1=V_{P.MNBC}+V_{P.BMQ}$

$\frac{V_{P.MNBC}}{V}=\frac{1}{3}.\frac{d\left(P;\left(ABC\right)\right)}{d\left(C\text{'};\left(ABC\right)\right)}.\frac{S_{MNPQ}}{S_{ABC}}$

$=\frac{1}{3}.\frac{PC}{C\text{'}C}.\frac{S_{ABC}-S_{AMN}}{S_{ABC}}$

     $=\frac{1}{3}.x.\frac{S_{ABC}-\frac{1}{4}{S}_{ABC}}{S_{ABC}}=\frac{1}{4}x$

$\frac{V_{P.BMQ}}{V}=\frac{V_{C\text{'}.BMQ}}{\frac{3}{2}{V}_{C\text{'}.ABB\text{'}A\text{'}}}=\frac{2}{3}\frac{S_{BMQ}}{S_{ABB\text{'}A\text{'}}}=\frac{2}{3}.\frac{\frac{1}{2}.x.S_{ABB\text{'}}}{2S_{ABB\text{'}}}=\frac{1}{6}x$

$\Rightarrow \frac{V_1}{V}=\frac{1}{4}x+\frac{1}{6}x=\frac{5}{12}x=\frac{1}{3}\iff x=\frac{4}{5}.$

Chọn C.