Trang chủ
Đề thi & kiểm tra
Toán học
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 3,...
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 3, BC = 2, AD' = căn bậc hai của 5
Câu hỏi :
Cho hình hộp chữ nhật ABCD.A'B'C'D' có Gọi I là trung điểm của BC. Khoảng cách từ D đến mặt phẳng (AID') bằng
Cho hình hộp chữ nhật ABCD.A'B'C'D' có Gọi I là trung điểm của BC. Khoảng cách từ D đến mặt phẳng (AID') bằng
A.
B.
C.
D.
* Đáp án
C
* Hướng dẫn giải
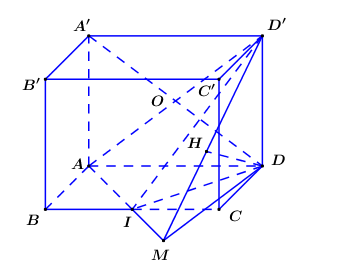
Gọi
Do đó .
Trong (ABCD) dựng trong (DD'M) dựng ta có:
Ta có
Lại có
Áp dụng định lí Pytago:
Áp dụng hệ thức lượng trong tam giác vuông DD'M có:
Vậy
Chọn C.Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Số câu hỏi: 1500
Copyright © 2021 HOCTAP247
