Trong mặt phẳng (anpha) cho hai tia Ox, Oy và góc xOy = 60 độ. Trên tia Oz vuông

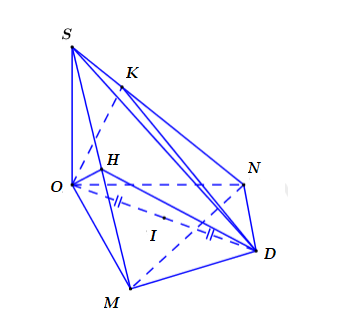
Gọi I là tâm đường tròn ngoại tiếp tam giác OMN, D' là điểm đối xứng với I qua O

Ta có:

$\left\{\begin{array}{l}DM\perp OM\\ DM\perp SO\end{array}\right.\Rightarrow DM\perp \left(SOM\right)\Rightarrow DM\perp OH$

$\left\{\begin{array}{l}OH\perp DM\\ OH\perp SM\end{array}\right.\Rightarrow OH\perp \left(SDM\right)\Rightarrow OH\perp HD$

$\Rightarrow \angle OHD={90}^0\Rightarrow IO=IH=ID.$

Chứng minh tương tự ta có $OK\perp \left(SDN\right)\Rightarrow OK\perp KD\Rightarrow \angle OKD={90}^0\Rightarrow IO=IK=ID.$

$\Rightarrow IO=IM=IN=IH=IK\Rightarrow I$ là tâm mặt cầu ngoại tiếp khối đa diện MNHOK.

Gọi P và Q là trung điểm OM và ON nên P và Q là tâm đường tròn ngoại tiếp tam giác OHM và OKN.

Ta có bán kính mặt cầu này là:

$R=IO=R_{\Delta OMN}=\frac{MN}{2\sin \angle MON}$

$=\frac{\sqrt{O{M}^2+O{N}^2-2OM.ON.\cos OMN}}{\sqrt{3}}=\frac{\sqrt{O{M}^2+O{N}^2-OM.ON}}{\sqrt{3}}$

Ta có: $O{M}^2+O{N}^2-OM.ON={\left(OM+ON\right)}^2-3OM.ON=a^2-3OM.ON$

Lại có $OM.ON\le \frac{{\left(OM+ON\right)}^2}{4}=\frac{a^2}{4}$ nên $O{M}^2+O{N}^2-OM.ON\ge a^2-3\frac{a^2}{4}=\frac{a^2}{4}.$

Do đó ta có $R\ge \frac{\sqrt{\frac{a^2}{4}}}{\sqrt{3}}=\frac{a}{2\sqrt{3}}.$

Vậy $S=4\pi R^2\ge 4\pi .{\left(\frac{a}{2\sqrt{3}}\right)}^2=\frac{\pi a^2}{3}.$

Chọn D.