Trang chủ
Đề thi & kiểm tra
Toán học
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Cho mặt cầu S(O; 4) cố định. Hình nón (N)...
Cho mặt cầu S(O; 4) cố định. Hình nón (N) gọi là nội tiếp mặt cầu nếu hình nón (N)
Câu hỏi :
Cho mặt cầu S(O; 4) cố định. Hình nón (N) gọi là nội tiếp mặt cầu nếu hình nón (N) có đường tròn đáy và đỉnh thuộc mặt cầu S(O; 4) .Tính bán kính đáy r của (N) để khối nón (N) có thể tích lớn nhất.
Cho mặt cầu S(O; 4) cố định. Hình nón (N) gọi là nội tiếp mặt cầu nếu hình nón (N) có đường tròn đáy và đỉnh thuộc mặt cầu S(O; 4) .Tính bán kính đáy r của (N) để khối nón (N) có thể tích lớn nhất.
A.
B.
C.
D.
* Đáp án
D
* Hướng dẫn giải
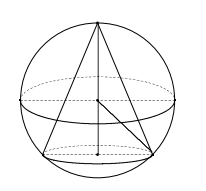
Gọi r, h lần lượt là bán kính đáy và chiều cao của hình nón (N). Dễ thấy lớn nhất thì
Áp dụng định lí Pytago ta có:
Xét hàm số với ta có:
BBT:
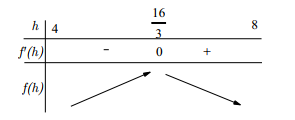
Dựa vào BBT ta thấy
Vậy đặt GTLN khi
Chọn D.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề) !!
Số câu hỏi: 1500
Copyright © 2021 HOCTAP247
