Trong hệ tọa độ Oxyz, cho tam giác ABC với A(1; -2; 3), B(-1; -2; 1), C(1; 0; 1)

* Hướng dẫn giải

Chọn D.

(S) có tâm I(1; -2; 1) và bán kính $R=\sqrt{1^2+{\left(-2\right)}^2+1^2-2}=2.$

Mà $AB=AC=BC=2\sqrt{2}$ hay tam giácABC đều. Và $A,B,C\in \left(S\right)$.

Gọi $G\left(\frac{1}{3};-\frac{4}{3};\frac{5}{3}\right)$ là trọng tâm tam giác ABC

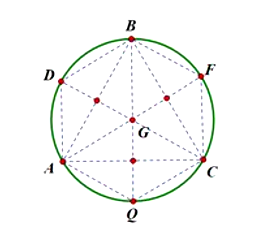
Xét đường tròn ngoại tiếp tam giác ABC. Kẻ các đường kính $CD,AF,BQ.$

Gọi J là hình chiếu vuông góc của M lên (ABC), J nằm trong hình lục giác đều ADBFCQ.

* Với J trùng với một trong 3 điểm A, B, C hay M trùng với một trong 3 điểm A, B, C.

Ta có $T=A{K}^2+B{E}^2+C{H}^2={\left(2\sqrt{2}\right)}^2+0^2+{\left(\sqrt{2}\right)}^2=10$

* Với J không trùng với 3 điểm A, B, C

Ta có $T=A{K}^2+B{E}^2+C{H}^2\ge \frac{{\left(AK+BE+CH\right)}^2}{3}=\frac{{\left(3\sqrt{2}\right)}^2}{3}=6.$

Dấu bằng xảy ra khi $AK=BE=CH.$

Suy ra $T_{\min }=6$ khi J trùng với trọng tâm G của tam giác ABC hay $MA=MB=MC.$

Vậy có 2 điểm M cần tìm.