Cho các số phức z1, z2, z3 thỏa mãn |z1| = |z2| = 2|z3| = 2 và 3z1z2 = 4z3(z1 + z2).

* Hướng dẫn giải

Đáp án đúng là: A

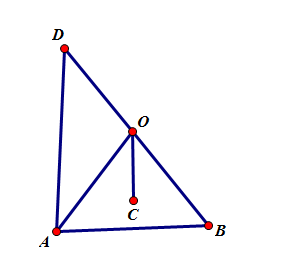
Ta có 3z₁z₂ = 4z₃(z₁ + z₂) Þ |3z₁z₂| = |4z₃(z₁ + z₂)|

Û |3z₁z₂| = |4z₃(z₁ - (-z₂))|

Û |z₁ - (-z₂)| = 3

Lấy D đối xứng với B qua O, suy ra D biểu diễn (-z₂).

Ta có |z₁ - (-z₂)| = 3 Û AD = 3

DABD có trung tuyến  nên DABD vuông tại A

$\Rightarrow AB=\sqrt{B{D}^2-A{D}^2}=\sqrt{7}$

+) 3z₁z₂ = 4z₃(z₁ + z₂) Û z₁(3z₂ - 4z₃) = 4z₂z₃

Þ |z₁||3z₂ - 4z₃| = |4z₂z₃|

Þ |3z₂ - 4z₃| = 4

$\iff 9O{B}^2+16O{C}^2-24OB.OC.\cos \widehat{BOC}=16$

$\iff \cos \widehat{BOC}=\frac{3}{4}$

Áp dụng định lí cosin cho DBOC ta có:

$BC=\sqrt{O{B}^2+O{C}^2-2OB.OC.\cos \widehat{BOC}}=\sqrt{4+1-4.\frac{3}{4}}=\sqrt{2}$

Tương tự ta tính được $AC=\sqrt{2}$

Vậy $S_{ABC}=\frac{\sqrt{7}}{4}.$