Có bao nhiêu giá trị nguyên âm của tham số a để hàm số

Đáp án đúng là: B

Xét g(x) = x⁴ + ax² − 8x

g'(x) = 4x³ + 2ax − 8

Xét g'(x) = 0 4x³ +2ax − 8 = 0 $\iff$ −a = = 2x² − = h(x) (do x = 0 không là nghiệm)

g(x) = 0$\iff$$\left[\begin{array}{c}x=0\\ x^3+ax-8=0\iff -a=\frac{x^3-8}{x}=x^2-\frac{8}{x}=k\left(x\right)\end{array}\right.$

h’(x) = 4x +$\frac{4}{x^2}$ = 0$\iff$ x = −1

k’(x) = 2x +$\frac{8}{x^2}$ = 0$\iff$ x =$\sqrt[3]{-4}$

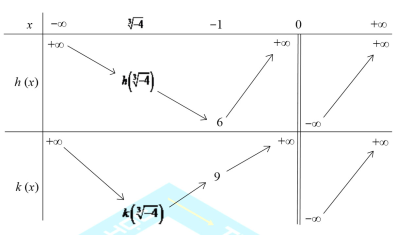
Để hàm số y = |g(x)| có đúng 3 cực trị −a  ≤ 6 Û a  ≥ −6

Mà a là số nguyên âm nên a Î {−6; −5; −4; −3; −2; −1}