Trang chủ
Đề thi & kiểm tra
Toán học
Giải Đề thi THPT Quốc gia môn Toán năm 2022 (4 mã đề gốc) !!
Cho hàm số bậc bốn y = f(x). Biết rằng...
Cho hàm số bậc bốn y = f(x). Biết rằng hàm số g(x) = ln f(x) có bảng
Câu hỏi :
Cho hàm số bậc bốn y = f(x). Biết rằng hàm số g(x) = ln f(x) có bảng biến thiên như sau
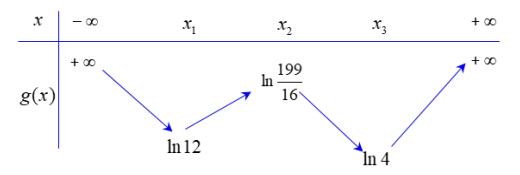
Diện tích hình phẳng giới hạn bởi các đường y = f'(x) và y = g'(x) thuộc khoảng nào dưới đây?
Cho hàm số bậc bốn y = f(x). Biết rằng hàm số g(x) = ln f(x) có bảng biến thiên như sau

Diện tích hình phẳng giới hạn bởi các đường y = f'(x) và y = g'(x) thuộc khoảng nào dưới đây?
A. (7; 8).
B. (6; 7).
C. (8; 9).
D. (10; 11).
* Đáp án
* Hướng dẫn giải
Đáp án đúng là: A
Từ bảng biến thiên của g(x) ta có ln f(x) ≥ ln 4 Û f(x) ≥ 4; ∀x Î ℝ.
Ta có g'(x) = .
Xét phương trình f'(x) = g'(x) Û f'(x) = .
Û
Do f(x) ≥ 4; ∀x Î ℝ nên phương trình (**) vô nghiệm.
Từ đó suy ra f'(x) = 0 Û g'(x) = 0 Û .
Mặt khác f'(x) – g'(x) = f'(x)..
Ta có bảng xét dấu
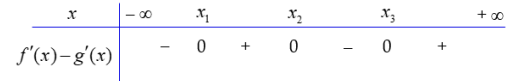
Vậy S =
=
= f(x2) – g(x2) – f(x1) + g(x1) – f(x3) + g(x3) + f(x2) – g(x2)
= 2f(x2) – f(x1) – f(x3) – 2ln f(x2) + ln f(x1) + ln f(x3)
= 2.−12 – 4 – 2ln+ ln 12 + ln 4 ≈ 7,704 Î (7; 8).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Đề thi THPT Quốc gia môn Toán năm 2022 (4 mã đề gốc) !!
Số câu hỏi: 200
Copyright © 2021 HOCTAP247
