Trong không gian Oxyz, cho điểm A(2; 1; 1). Gọi (P) là mặt phẳng chứa

Đáp án đúng là: C

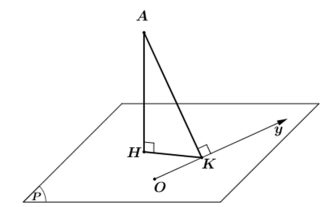
Gọi H và K lần lượt là hình chiếu của A trên (P) và trục Oy.

Với A(2; 1; 1) ta có hình chiếu của A lên Oy là K(0; 1; 0).

Ta có d(A, (P)) = AH ≤ AK.

Do đó khoảng cách từ A đến (P) lớn nhất khi H ≡ K(0; 1; 0).

Khi đó (P) đi qua K(0; 1; 0) và có một vectơ pháp tuyến là $\overrightarrow{AK}$= (−2; 0; −1) = −(2; 0; 1) nên có phương trình là 2x + z = 0.