Bài tập 19 trang 167 SBT Toán 6 Tập 1
Bài tập 19 trang 167 SBT Toán 6 Tập 1
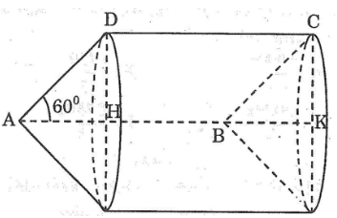
Cho hình bình hành ABCD với AB=1,AD=x (x > 0) và góc (BAD) = 60°
a) Tính diện tích toàn phần S của hình tạo thành khi quay hình bình hành ABCD đúng một vòng quanh cạnh AB và diện tích toàn phần S1 của hình tạo thành khi quay cạnh AD
b) Xác định giá trị x khi S = S1 và S = 2S1
a.*Khi quay hình bình hành ABCD một vòng quanh cạnh AB thì cạnh AD và BC vạch nên hai hình nón bằng nhau có đường sinh AD = BC = x, cạnh CD vạch nên hình trụ có bán kính đáy bằng bán kính hình nón
Trong tam giác AHD,ta có:
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ
*Khi quay hình bình hành ABCD một vòng quanh AD thì cạnh AB và DC vạch nên hai hình nón bằng nhau có đường sinh AD = BC = 1, cạnh CD vạch nên hình trụ có bán kính đáy bằng bán kính hình nón
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ
S1 = 2πDH.AB + 2πDH.AD =
= π.√3 +π.x.√3 = π.√3 (x+1) (đvdt)
b.*Ta có: S = S1 ⇔ π.x.√3 (1+x) = π.√3 (x+1)
⇔ x(1+x) = x +1 ⇔ x2 -1 =0 ⇔ (x+1)(x-1) = 0
Vì x > 0 nên x+1 > 0
suy ra: x-1 = 0 ⇔ x = 1
*Ta có: S = 2S1 ⇔ .x.√3 (1+x) = 2.π.√3 (x+1)
⇔ x(x+1) = 2(x+1) ⇔ x2 – x -2 =0
⇔ x2 – 2x +x - 2 = 0 ⇔ (x+1)(x-2) = 0
Vì x > 0 nên x+1 > 0
suy ra : x-2 = 0 ⇔ x = 2
-- Mod Toán 9
Copyright © 2021 HOCTAP247