Bài tập 36 trang 126 SGK Toán 9 Tập 2
Bài tập 36 trang 126 SGK Toán 9 Tập 2
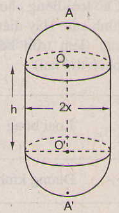
Một chi tiết máy gồm một hình trù và hai nửa hình cầu với các kích thước đã cho trên hình 111 (đơn vị: cm)
a) Tìm một hệ thức giữa x và h khi AA' có độ dài không đổi và bằng 2a.
b) Với điều kiện ở a) hãy tính diện tích bề mặt và thể tích của chi tiết theo x và a.
Bài 36 yêu cầu chúng ta tính thể tích của bề mặt và chi tiết theo các độ dài đại số là các biến số.
Câu a:
Ta có hệ thức liên hệ giữa x và h là:
\(\small h + 2x = 2a\)
Câu b:
Diện tích cần tính gồm diện tích xung quanh của hình trụ có bán kính đáy là x, chiều cao là h và diện tích mặt cầu có bán kính là x.
Diện tích xung quanh của hình trụ:
\(\small S_t=2\pi.x.h\)
Diện tích mặt cầu:
\(\small S_c=4.\pi.x^2\)
Nên diện tích bề mặt của chi tiết máy là:
\(\small S=S_t+S_c=2\pi.x.h+4\pi.x^2=2\pi.x.(h+2x)=4\pi.a.x\)
Thể tích cần tình gồm thể tích hình trù và thể tích hình cầu. Ta có:
\(\small V_t=\pi.x^2.h\)
\(\small V_c=\frac{4}{3}\pi.x^3\)
Nên thể tích của chi tiết máy là:
\(\small V=V_t+V_c=\pi.x^2.h+\frac{4}{3}.\pi.x^3=2\pi.x^2.a-\frac{2}{3}\pi.x^3\)
-- Mod Toán 9
Copyright © 2021 HOCTAP247
