Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
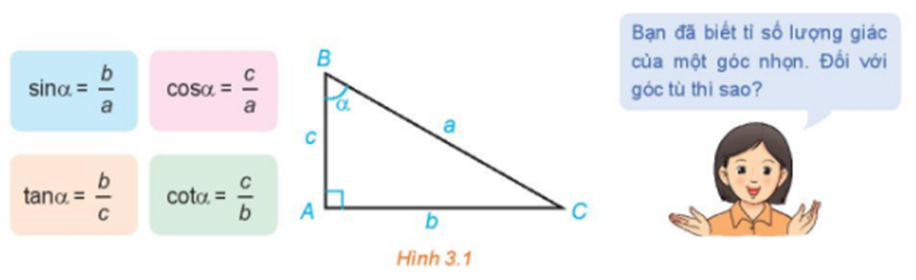
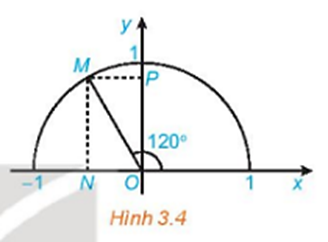
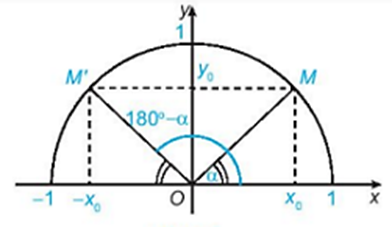
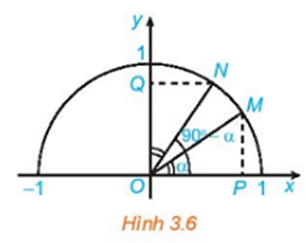
Bài tập Giá trị lượng giác của một góc từ 0 độ đến 180 độ có đáp án !!
Bài tập Giá trị lượng giác của một góc từ 0 độ đến 180 độ có đáp án !!
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247