Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Trắc nghiệm Toán 10 CTST Bài tập ôn tập chương 4 có đáp án (Phần 2) !!
Trắc nghiệm Toán 10 CTST Bài tập ôn tập chương 4 có đáp án (Phần 2) !!
Câu 1 :
Với điểm \[M\left( {\frac{4}{5};\frac{3}{5}} \right)\], ta gọi \(\widehat {xOM} = \alpha \). Khẳng định nào sau đây đúng?
A. \[\sin \alpha = \frac{3}{5}\] và \(co{\rm{s}}\alpha \,{\rm{ = }}\frac{4}{5};\)
B. \[\sin \alpha = \frac{4}{5}\] và \[co{\rm{s}}\alpha \,{\rm{ = }}\frac{3}{5};\]
C. \[\sin \alpha = \frac{{16}}{{25}}\] và \(co{\rm{s}}\alpha \,{\rm{ = }}\frac{9}{{25}}\);
D. \[\sin \alpha = \frac{9}{{25}}\] và \[co{\rm{s}}\alpha \,{\rm{ = }}\frac{{16}}{{25}}.\].
Câu 2 : Với mọi góc α thỏa mãn 0° ≤ α ≤ 180°, ta luôn có sin(90° – α) và tan(90° – α) lần lượt bằng:
A. cotα và cosα;
B. sinα và tanα;
C. cosα và cotα;
D. cosα và tanα.
Câu 3 : Với mọi góc α thỏa mãn 0° ≤ α ≤ 180°, ta luôn có cos(180° – α) bằng:
A. –cosα;
B. cosα;
C. sinα;
D. tanα.
Câu 4 :
Giá trị của tan103° bằng:
A. tan77°;
B. –tan77°;
C. cot77°;
D. –cot77°.
Câu 5 :
Nếu góc α thỏa mãn 90° ≤ α ≤ 180° thì:
A. cotα > 0;
B. tanα > 0;
C. cosα > 0;
D. sinα > 0.
Câu 6 :
Cho tam giác ABC bất kì có BC = a, AC = b và AB = c. Đẳng thức nào đúng?
A. b2 = a2 + c2 – ac.cosB;
B. a2 = b2 + c2 + 2bc.cosA;
C. c2 = b2 + a2 + ab.cosC;
D. c2 = b2 + a2 – 2ab.cosC.
Câu 7 : Cho tam giác ABC có AB = c, BC = a và AC = b. Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Trong các mệnh đề sau, mệnh đề nào sai?
A. \(\frac{a}{{\sin A}} = 2R;\)
B. 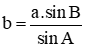 .
.
C. b = 2R.sinA;
D. c = 2R.sinC.
Câu 8 : Cho tam giác ABC bất kì có BC = a, AC = b và AB = c. Gọi ha, hb, hc độ dài các đường cao lần lượt ứng với các cạnh BC, CA, AB. Biết tam giác ABC có diện tích là S. Khẳng định nào sau đây là đúng?
A. ha = \(\frac{S}{a};\)
B. hb = \(\frac{{2S}}{b};\)
C. hc = \(\frac{S}{{2c}};\)
D. ha = \(\frac{{4S}}{a}.\)
Câu 9 : Cho tam giác ABC bất kì có BC = a, AC = b và AB = c. Gọi R, r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp tam giác; p, S lần lượt là nửa chu vi và diện tích tam giác. Khẳng định nào sau đây là đúng?
A. S = \(\frac{1}{2}\)abc;
B. \(\frac{a}{{\sin A}} = R;\)
C. \(\cos B = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\)
D. \(r = \frac{S}{p}.\)
Câu 10 : Cho tam giác ABC có BC = a, AC = b và AB = c. Biết \(\widehat C = 120^\circ .\) Khẳng định nào sau đây là đúng?
A. c2 = a2 + b2 – ab;
B. c2 = a2 + b2 + ab;
C. c2 = a2 + b2 – 3ab;
D. c2 = a2 + b2 + 3ab.
Câu 11 : Giá trị của biểu thức B = 3 – sin290° + 2cos260° – 3tan245° bằng:
A. 2;
B.\(\frac{1}{2}\);
C. \( - \frac{1}{2}\);
D. 0.
Câu 12 :
Cho hai góc α và β (với 0° ≤ α, β ≤ 180°) thỏa mãn α + β = 180°. Giá trị của biểu thức P = sinα.cosα + sinβ.cosβ bằng:
A. 0;
B. 1;
C. –1;
D. 2.
Câu 13 : Giá trị của biểu thức M = sin50° + cos70° + cos110° – sin130° bằng:
A. –1;
B. \(\frac{1}{2}\);
C. 0;
D. 1;
Câu 14 : Giá trị của biểu thức H = cot5°.cot10°.cot15°…cot80°.cot85° bằng:
A. –1;
B. 1;
C. 0;
D. 2.
Câu 15 : ∆ABC có AB = 3, AC = 6 và \(\widehat A = 60^\circ \). Độ dài bán kính R của đường tròn ngoại tiếp ∆ABC bằng:
A. 3;
B. \(3\sqrt 3 \);
C. \(\sqrt 3 \);
D. 6.
Câu 16 : ∆ABC có AB = 5, AC = 10, \(\widehat A = 60^\circ \). Độ dài đường cao ha của ∆ABC bằng:
A. \(3\sqrt 5 \);
B. \(\sqrt 5 \);
C. 5;
D. \(\frac{3}{2}\).
Câu 17 : Cho hình thoi ABCD có cạnh bằng 1 cm và có đường chéo AC = \(\sqrt 3 \) cm. Số đo \(\widehat {BAD}\) bằng:
A. 30°;
B. 45°;
C. 60°;
D. 120°.
Câu 18 : Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng:
A. 13 cm2;
B. \(13\sqrt 2 \) cm2;
C. \(12\sqrt 3 \) cm2;
D. 15 cm2.
Câu 19 :
Cho ∆ABC biết b = 32, c = 45, \[\widehat A = 87^\circ \]. Khẳng định nào sau đây đúng?
Cho ∆ABC biết b = 32, c = 45, \[\widehat A = 87^\circ \]. Khẳng định nào sau đây đúng?
A. a ≈ 53,8, \(\widehat B \approx 37^\circ ,\,\,\widehat C \approx 56^\circ \) ;
B. a ≈ 2898,3, \(\widehat B \approx 37^\circ ,\,\,\widehat C \approx 56^\circ \);
C. a ≈ 53,8, \(\widehat B \approx 56^\circ ,\,\,\widehat C \approx 37^\circ \);
D. a ≈ 55,2, \(\widehat B \approx 37^\circ ,\,\,\widehat C \approx 56^\circ \);.
Câu 20 : Cho ∆ABC, biết \(\widehat A = 60^\circ \), \({h_c} = 2\sqrt 3 \), R = 6. Khẳng định nào sau đây đúng?
A. \(a = 6\sqrt 3 ,\,\,b = 2 + 4\sqrt 6 ,c = 4;\);
B. \(a = 6\sqrt 3 ,\,\,b = 4,\,\,c = 2 + 4\sqrt 6 \);
C. \(a = 6\sqrt 3 ,\,\,b = 4,c = 2 + \sqrt 6 ;\)
D. \(a = 6\sqrt 3 ,\,\,b = 2 + \sqrt 6 ,c = 4\).
Câu 21 : Cho biết tanα = –3 (0° ≤ α ≤ 180°). Giá trị của \(H = \frac{{6\sin \alpha - 7\cos \alpha }}{{6\cos \alpha + 7\sin \alpha }}\) bằng:
A. \(\frac{4}{3}\);
B. \( - \frac{5}{3}\);
C. \( - \frac{4}{3}\);
D. \(\frac{5}{3}\).
Câu 22 : Cho biết sinα – cosα = \(\frac{1}{{\sqrt 5 }}\)(0° ≤ α, β ≤ 180°). Giá trị của \(E = \sqrt {{{\sin }^4}\alpha + {{\cos }^4}\alpha } \) bằng:
A. \(\frac{{\sqrt {15} }}{5}\);
B. \(\frac{{\sqrt {17} }}{5}\);
C. \(\frac{{\sqrt {19} }}{5}\);
D. \(\frac{{\sqrt {21} }}{5}\).
Câu 23 : Cho biết \(2\cos \alpha + \sqrt 2 \sin \alpha = 2\), với 0° < α < 90°. Giá trị của cotα bằng:
A. \(\frac{{\sqrt 5 }}{4}\);
B. \(\frac{{\sqrt 3 }}{4}\);
C. \(\frac{{\sqrt 2 }}{2}\);
D. \(\frac{{\sqrt 2 }}{4}\).
Câu 24 :
Cho ∆ABC và các khẳng định sau:
(I) b2 – c2 = a(b.cosC – c.cosB);
(II) (b + c)sinA = a(sinB + sinC);
(III) ha = 2R.sinB.sinC;
(IV) S = R.r.(sinA + sinB + sin C);
Số khẳng định đúng là:
Cho ∆ABC và các khẳng định sau:
(I) b2 – c2 = a(b.cosC – c.cosB);
(II) (b + c)sinA = a(sinB + sinC);
(III) ha = 2R.sinB.sinC;
(IV) S = R.r.(sinA + sinB + sin C);
Số khẳng định đúng là:
A. 1;
B. 2;
C. 3;
D. 4.
Câu 25 : Cho ∆ABC thỏa mãn \[\sin A = \frac{{\sin B + \sin C}}{{\cos B + \cos C}}\]. Khi đó ∆ABC là:
A. Tam giác vuông;
B. Tam giác cân;
C. Tam giác tù;
D. Tam giác đều.
Câu 26 : Cho ∆ABC có a.sinA + b.sinB + c.sinC = ha + hb + hc. Khi đó ∆ABC là:
A. Tam giác cân;
B. Tam giác đều;
C. Tam giác thường;
D. Tam giác vuông.
Câu 27 : Từ vị trí A, người ta quan sát một cái cây cao mọc vuông góc với mặt đất như hình vẽ.
A. 17,5 m;
B. 17 m;
C. 16,5 m;
D. 16 m.
Câu 28 : Giả sử CD = h là chiều cao của tháp, trong đó C là chân tháp.
A. 18 m;
B. 18,5 m;
C. 60 m;
D. 60,5 m.
Câu 29 : Trên nóc một tòa nhà có một cột ăng-ten cao 5 m. Từ vị trí quan sát A cao 7 m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50° và 40° so với phương nằm ngang.
A. 12 m;
B. 19 m;
C. 24 m;
D. 29 m.
Câu 30 : Từ hai vị trí A và B của một tòa nhà, người ta quan sát được đỉnh C của ngọn núi. Biết rằng độ cao của tòa nhà là AB = 70 m, phương nhìn AC tạo với phương ngang AH một góc bằng 30°, phương nhìn BC tạo với phương ngang BD một góc bằng 15°30’.
A. 135 m;
B. 234 m;
C. 165 m;
D. 195 m.
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247
