Bài tập 6 trang 156 SBT Toán 8 Tập 1
Bài tập 6 trang 156 SBT Toán 8 Tập 1
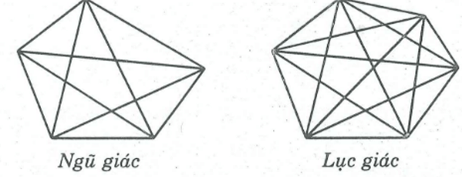
a) Vẽ hình và tính số đường chéo của ngũ giác, lục giác
b) Chứng minh rằng hình n-giác có tất cả \(\frac{{n\left( {n - 3} \right)}}{2}\) đường chéo.
a) Từ mỗi đỉnh của ngũ giác vẽ được 2 đường chéo. Ngũ giác có 5 đỉnh ta kê được 5.2=10 đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy ngũ giác có tất cả 5 đường chéo.
Từ mỗi đỉnh của lục giác vẽ được 3 đường chéo. Lục giác có 6 đỉnh ta kẻ được 6.3 = 18 đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy lục giác có tất cả 9 đường chéo.
b) Từ mỗi đỉnh của n-giác nối với các đình còn lại ta được n – l đoạn thẳng, trong đó có 2 đoạn thắng là cạnh của hình n-giác (hai đoạn thẳng nối với hai đỉnh kề nhau).
Vậy qua mỗi đỉnh n-giác vẽ được n-3 đường chéo. Hình n-giác có n đỉnh kẻ được n(n- 3) đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy hình n-giác có tất cả \(\frac{{n\left( {n - 3} \right)}}{2}\) đường chéo.
-- Mod Toán 8
Copyright © 2021 HOCTAP247