Bài tập 3.3 trang 161 SBT Toán 8 Tập 1
Bài tập 3.3 trang 161 SBT Toán 8 Tập 1
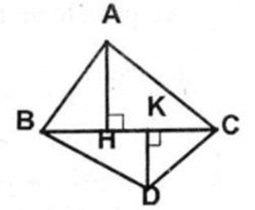
a) Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC
Chứng minh rằng \(\frac{{S'}}{S} = \frac{{DK}}{{AH}}\)
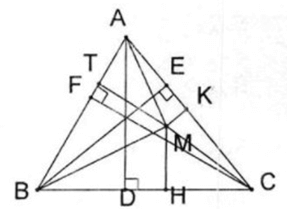
b) Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và song song với CF cắt cạnh BA tại điểm T.
Chứng minh rằng \(\frac{{MH}}{{AD}} = \frac{{MK}}{{BE}} + \frac{{MT}}{{CF}} = 1\)
a) Hai ΔABC và ΔDBC có chung canh đáy BC nên ta có:
SABC = \(\frac{1}{2}\) AH. BC = S
SDBC = \(\frac{1}{2}\) DK. BC = S'
\( \Rightarrow \frac{{S'}}{S} = \frac{{\frac{1}{2}DK.BC}}{{\frac{1}{2}AH.BC}} = \frac{{DK}}{{AH}}\)
b. Gọi diện tích các hình tam giác ABC, MAB, MAC, MBC lần lượt là S; S1; S2 ; S3. Ta có:
S = S1 + S2 + S3
Trong đó: S = \(\frac{1}{2}\) AD.BC = \(\frac{1}{2}\) BE. AC = \(\frac{1}{2}\) CF. AB
S1 = \(\frac{1}{2}\) MT. AB
S2 = \(\frac{1}{2}\) MK. AC
S3 = \(\frac{1}{2}\) MH. BC
\(\begin{array}{l}
\frac{{{S_1}}}{S} = \frac{{\frac{1}{2}MT.AB}}{{\frac{1}{2}CF.AB}} = \frac{{MT}}{{CF}}\\
\frac{{{S_2}}}{S} = \frac{{\frac{1}{2}MK.AC}}{{\frac{1}{2}BE.AC}} = \frac{{MK}}{{BE}}\\
\frac{{{S_3}}}{S} = \frac{{\frac{1}{2}MH.BC}}{{\frac{1}{2}AD.BC}} = \frac{{MH}}{{AD}}\\
\Rightarrow \frac{{MH}}{{AD}} = \frac{{MK}}{{BE}} + \frac{{MT}}{{CF}}\\
= \frac{{{S_3}}}{S} + \frac{{{S_2}}}{S} + \frac{{{S_1}}}{S}\\
= \frac{{{S_1}}}{S} + \frac{{{S_1}}}{S} + \frac{{{S_1}}}{S} = 1
\end{array}\)
-- Mod Toán 8
Copyright © 2021 HOCTAP247