Bài tập 30 trang 126 SGK Toán 8 Tập 1
Bài tập 30 trang 126 SGK Toán 8 Tập 1
Trên hình 143 ta có hình thang ABCD với đường trung bình EF và hình chữ nhật GHIK. Hãy so sánh dện tích hai hình này, từ đó suy ra một cách chứng minh khác về công thức diện tích hình thang.
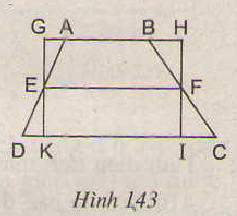
Ta có hình thang ABCD ( AB// CD), với đường trung bình EF và hình chữ nhật GHIK như hình vẽ .
Dễ dàng chứng minh
\(\Delta AEK = \Delta DEK, \Delta EFH = \Delta CFI\)
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên
SABCD = SGHIK = EF. AJ mà \(EF = \frac{AB+CD}{2}\)
Do đó \(S_{ABCD}= \frac{AB+CD}{2}\) ( AB + CD). AJ
Vậy ta gặp lại công thức tính diện tích hình thang đã được học nhưng bằng một phương pháp chứng minh khác. Mặt khác, ta phát hiện công thức mới : Diện tích hình thang bằng tích của đường trung bình hình thang với chiều cao.
-- Mod Toán 8
Copyright © 2021 HOCTAP247
