Bài tập 40 trang 162 SBT Toán 8 Tập 1
Bài tập 40 trang 162 SBT Toán 8 Tập 1
Hai cạnh của một hình hình hành có độ dài là 6cm và 8cm. Một trong các đường cao có độ dài là 5cm. Tính độ dài đường cao thứ hai. Hỏi bài toán có mấy đáp số.
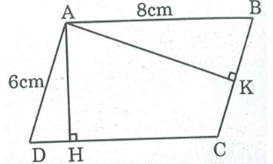
Giả sử hình bình hành ABCD cói AB = 8cm, AD = 6cm.
Kẻ AH ⊥ CD, AK ⊥ BC.Ta có 5 < 6, 5 < 8
Đường cao là cạnh góc vuông nhỏ hơn cạnh huyền thỏa mãn có hai trường hợp:
*Trường hợp 1: AK = 5cm
Ta có: SABCD = AK.BC = 5.6 = 30 (cm2)
SABCD = AH.AD = 8.AH
Suy ra: 8.AH = 30 ⇒ AH = \(frac{{30}}{8}\) = \(frac{{15}}{4}\) (cm)
*Trường hợp 2: AH = 5cm
Ta có: SABCD = AH.CD= 5.8 = 40 (cm2)
SABCD = AK.BC = 6.AH
Suy ra: 6.AK = 40 ⇒ AK = \(frac{{40}}{6}\) = \(frac{{20}}{3}\) (cm)
Vậy đường cao thứ hai có độ dài là \(frac{{15}}{4}\) cm hoặc \(frac{{20}}{3}\) cm
Bài toán có 2 đáp số.
-- Mod Toán 8
Copyright © 2021 HOCTAP247