Trang chủ
Lớp 8
Toán Lớp 8 SGK Cũ
Chương 2: Đa Giác. Diện Tích Đa Giác
Bài tập 3.2 trang 161 SBT Toán 8 Tập 1
Bài tập 3.2 trang 161 SBT Toán 8 Tập 1
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 3.2 trang 161 SBT Toán 8 Tập 1
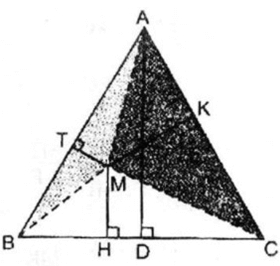
Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H. Đường thẳng đi qua điểm M và vuông góc với CA tại điểm K. Đường thẳng đi qua điểm M và vuông góc với AB tại điểm T.
Giả sử ΔABC đều có cạnh bằng a, kẻ đường cao AD, đặt AD = h không đổi.
Ta có:
SABC = \(\frac{1}{2}\) ah
SMAB = \(\frac{1}{2}\) MT.a
SMAC = \(\frac{1}{2}\) MK.a
SMBC = \(\frac{1}{2}\) MH.a
SABC = SMAB + SMAC+ SMBC
\(\frac{1}{2}\) a.h = \(\frac{1}{2}\) MT.a + \(\frac{1}{2}\)MK.a + \(\frac{1}{2}\) MH.a
\(\frac{1}{2}\) a. (MT + MK + MH)
=> MT + MK + MH = h không đổi
Vậy tổng MT + MK + MH không phụ thuộc vào điểm M.
-- Mod Toán 8
Copyright © 2021 HOCTAP247