Bài tập 61 trang 83 SGK Toán 7 Tập 2
Bài tập 61 trang 83 SGK Toán 7 Tập 2
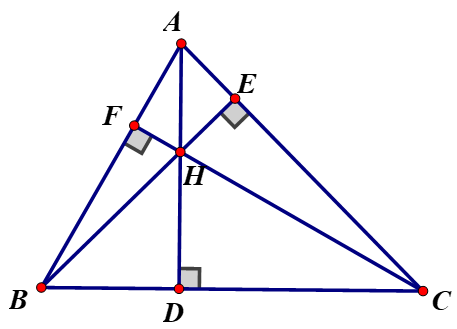
Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.
b) Tương tự, hãy lần lượt chỉ ra trực tâm của tam giác HAB và HAC.
Các đường thẳng HA, HB, HC lần lượt cắt cạnh đối BC, AC, AB tại N, M, E.
a) ΔHBC có:
HN ⊥ BC nên là đường cao
BE ⊥ HC nên là đường cao
CM ⊥ BH nên CM là đường cao
Mà là giao điểm của các đường thẳng HN, BE, C nên là trực tâm của ΔHBC
b) ΔAHB
HE ⊥ AB nên HE là đường cao
BC ⊥ AH nên là đường cao
AC ⊥ BH nên là đường cao
Mà C là giao điểm của các đường HE, BC, AC nên C là trực tâm của ΔAH
ΔAHC
HM ⊥ AC nên là đường cao
AB ⊥ nên là đường cao
CB ⊥ AH nên CB là đường cao
Mà là giao điểm của các đường HM, AB, CB nên là trực tâm của ΔAH.
-- Mod Toán 7
Copyright © 2021 HOCTAP247