Bài tập 62 trang 83 SGK Toán 7 Tập 2
Bài tập 62 trang 83 SGK Toán 7 Tập 2
Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
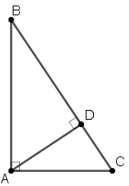
+ TH1: Xét ΔABC vuông tại A có các đường cao AD, BA, CA.
BA, CA là hai đường cao xuất phát từ hai góc nhọn B và C của ΔABC.
AB = AC => ΔABC cân tại A (đpcm).
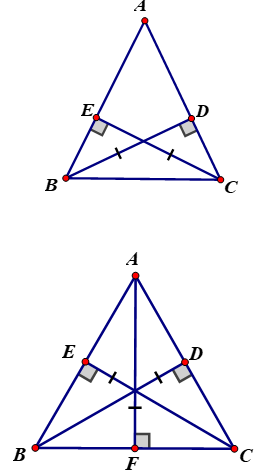
+ TH2: Xét ΔABC không có góc nào vuông, hai đường cao BD = CE (như hình vẽ minh họa)
Xét hai tam giác vuông EBC và DCB có:
BC (cạnh chung)
CE = BD (giả thiết)
=> ∆EBC = ∆DCB (cạnh huyền - cạnh góc vuông)
Suy ra \(\widehat {EBC} = \widehat {DCB}\) (hai góc tương ứng)
Hay \(\widehat {ABC} = \widehat {ACB} \Rightarrow \Delta ABC\) cân tại A
+ Xét ΔABC ba đường cao BD = CE = AF (như hình vẽ minh họa)
CE = BD => ΔABC cân tại A (như cmt) => AB = AC.
CE = AF => ΔABC cân tại B (như cmt) => AB = BC:
=> AB = AC = BC
=> ΔABC đều.
-- Mod Toán 7
Copyright © 2021 HOCTAP247