Chương 2: Hàm Số Bậc Nhất Và Bậc Hai

Tìm tập xác định của các hàm số sau:

a) \(y= \frac{3x-2}{2x+1};\)

b) \(y= \frac{x-1}{x^{2}+2x-3};\)

c) \(y= \sqrt{2x+1}-\sqrt{3-x}.\)

 Cho hàm số \(y = \left\{ \begin{array}{l}
x + 1,{\rm{ }}x \ge 2\\
{x^2} - 2,{\rm{ }}x < 2
\end{array} \right.\)

Tính giá trị của hàm số tại \(x = 3, x = - 1, x = 2\).

Cho hàm số \(y = 3 x^2 - 2x + 1\). Các điểm sau có thuộc đồ thị hay không?

a) M (- 1;6);

b) N (1;1);

c) P(0;1).

Xét tính chẵn lẻ của hàm số: 

a) \(y = |x|\);

b) \(y = (x + 2)^2\)     

c) \(y = x^3 + x\) ;

d) \(y = x^2 + x + 1\).

Vẽ đồ thị hàm số:

a) \(y = 2x - 3\);

b) \(y = \sqrt{2}\);

c) \(y=-\frac{3x}{2}+7;\)

d) \(y = |x|-1\).

Xác định a, b để đồ thị của hàm số \(y = ax + b\) đi qua các điểm.

a) \(A(0; 3)\) và \(B=(\frac{3}{5};0)\);

b) \(A(1; 2)\) và \(B(2; 1)\);

c) \(A(15;- 3)\) và \(B(21;- 3)\).

Viết phương trình \(y = ax + b\) của đường thẳng:

a) Đi qua điểm \(A(4; 3), B(2;- 1)\).

b) Đi qua điểm \(A(1;- 1)\) và song song với Ox.

Vẽ đồ thị hàm số.

a) \(y=\left\{\begin{matrix} 2x \ \ voi \ \ x\geq 0\\ \\ -\frac{1}{2}x \ \ voi \ \ x<0 \end{matrix}\right.\)

b) \(y=\left\{\begin{matrix} x+1 \ \ voi \ \ x\geq 1\\ \\ -2x+4 \ \ voi \ \ x<1 \end{matrix}\right.\) 

Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của mỗi parabol.

a) \(y = x^2 - 3x + 2\);                b) \(y = - 2x^2 + 4x - 3\);

c) \(y = x^2 - 2x\);                        d) \(y = - x^2 + 4\). 

Lập bảng biến thiên và vẽ đồ thị của các hàm số.

a) ^{\(y = 3x^2- 4x + 1\)};                      b) \(y = - 3x^2 + 2x - 1\);

c) \(y = 4x^2- 4x + 1\);                      d) \(y = - x^2 + 4x - 4\);

e) \(y = 2x^2+ x + 1\);                       f) \(y = - x^2 + x - 1\).

Xác định parabol \(y = ax^2 + bx + 2\), biết rằng parabol đó:

a) Đi qua hai điểm \(M(1; 5)\) và \(N(- 2; 8)\);

b) Đi qua hai điểm \(A(3;- 4)\) và có trục đối xứng là x=

c) Có đỉnh là \(I(2;- 2)\);

d) Đi qua điểm \(B(- 1; 6)\) và tung độ của đỉnh là 

 Xác định a, b, c, biết parabol \(y = ax^2 + bx + c\) đi qua điểm A(8; 0) và có đỉnh I(6; - 12).

Phát biểu quy ước về xác định của hàm số cho bởi công thức. Từ đó hai hàm số \(y = \frac{{x + 1}}{{(x + 1)({x^2} + 2)}}\) và \(y = \frac{1}{{{x^2} + 2}}\) có gì khác nhau?

Thế nào là hàm số đồng biến (nghịch biến) trên khoảng (a; b)?

Thế nào là một hàm số chẵn? Thế nào là một hàm số lẻ?

Chỉ ra khoảng đồng biến, khoảng nghịch biến của hàm số y = ax + b, trong mỗi trường hợp a > 0; a < 0.

Chỉ ra khoảng đồng biến, khoảng nghịch biến của hàm số: \(y = {\rm{a}}{{\rm{x}}^2} + bx + c,\) trong mỗi trường hợp a > 0, a < 0. 

Xác định toạ độ của đỉnh, phương trình của trục đối xứng của parabol \(y = {\rm{a}}{{\rm{x}}^2} + bc + c.\)

Xác định toạ độ giao điểm của parabol \(y = {\rm{a}}{{\rm{x}}^2} + bc + c\) với trục tung. Tìm điều kiện để parabol này cắt trục hoành tại hai điểm phân biệt, tại một điểm và viết toạ độ của các giao điểm trong mỗi trường hợp.

Tìm tập xác định của các hàm số

a) \(y = \frac{2}{{x + 1}} + \sqrt {x + 3} \)

b) \(y = \sqrt {2 - 3x}  - \frac{1}{{\sqrt {1 - 2x} }}\)

c) \(y = \left\{ \begin{array}{l}\frac{1}{{x + 3}}\,\,\,\,\,\,\,\,\,\,\,\,\,voi\,\,\,\,x \ge 1\\\sqrt {2 - x} \,\,\,\,\,\,\,\,\,voi\,x < 1\end{array} \right.\)

Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau:

a) \(y = \frac{1}{2}x - 1\)                   b) \(y = 4 - 2x\)

c) \(y = \sqrt {{x^2}} \)                      d) \(y = \left| {x + 1} \right|\)  

Lập bảng biến thiên và vẽ đồ thị của các hàm số

a) \(y = {x^2} - 2x - 1;\)

b) \(y =  - {x^2} + 3x + 2\)

Xác định a, b biết đường thẳng y = ax + b đi qua hai điểm A(1; 3), B(-1; 5).

Xác định a, b, c biết parabol \(y = {\rm{a}}{{\rm{x}}^2} + bx + c\)

a) Đi qua ba điểm A(0; -1), B(1; -1); C(-1; 1)

b) Có đỉnh I(1; 4) và đi qua điểm D(3; 0).

Tìm tập xác định của hàm số sau:

a) \(y = \frac{{3x + 5}}{{{x^2} - x + 1}}\);                   

b) \(y = \frac{{x - 2}}{{{x^2} - 3x + 2}}\);

c) \(y = \frac{{\sqrt {x - 1} }}{{x - 2}}\);                       

d) \(y = \frac{{{x^2} - 2}}{{\left( {x + 2} \right)\sqrt {x + 1} }}\)

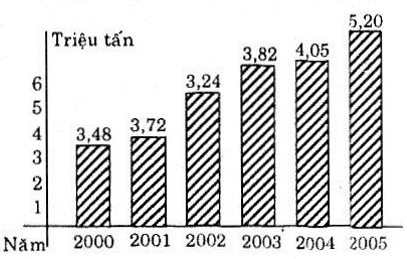
Biểu đồ ở hình bên cho biết số triệu tấn gạo xuất khẩu của Việt Nam trong các năm từ 2000 đến 2005. Biểu đồ này cho một hàm số. Hãy cho biết tập xác định và nêu một vài giá trị của hàm số đó

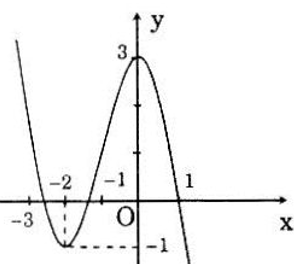
Hình bên là đồ thị của một hàm số có tập xác định là R. Dựa vào đồ thị hãy lập bảng biến thiên của hàm số

Khảo sát sự biến thiên của mỗi hàm số sau và lập bảng của nó:

a) \(y = x^2 + 2x - 2\) trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\);

b) \(y = - 2x^2 + 4x + 1\) trên mỗi khoảng \(\left( { - \infty ; -1} \right)\) và \(\left( {  1; + \infty } \right)\);

c) \(y = \frac{2}{{x - 3}}\) trên mỗi khoảng \(\left( { - \infty ; 3} \right)\) và \(\left( { 3; + \infty } \right)\)

Mỗi hàm số sau là hàm số chẵn hay hàm số lẻ?

a) y = x⁴ – 3x² + 1

b) y = - 2x³ + x

c) y = |x + 2| - |x – 2|

d) y = |2x + 1| + |2x – 1|

Cho đường thẳng (d): y = 0,5x. Hỏi ta sẽ được đồ thị của hàm số nào khi tịnh tiến (d):

a) Lên trên 3 đơn vị

b) Xuống dưới 1 đơn vị

c) Sang phải 2 đơn vị

d) Sang trái 6 đơn vị

Quy tắc đặt tương ứng mỗi số thực dương với căn bậc hai của nó có phải là một hàm số không? Vì sao?

Giả sử (G) là đồ thị của hàm số y = f(x) xác định trên tập D; A là một điểm trên trục hoành có hoành độ bằng a. Từ A, dựng đường thẳng (d) song song (hoặc trùng) với trục tung.

a) Khi nào thì (d) có điểm chung với (G).

b) (d) có thể có bao nhiêu điểm chung với (G)? Vì sao?

c) Đường tròn có thể là đồ thị của hàm số không? Vì sao?

Tìm tập xác định của mỗi hàm số sau:

a) \(y = \frac{{3x + 1}}{{{x^2} - 9}}\)                           

b) \(y = \frac{x}{{1 - {x^2}}} - \sqrt { - x} \)

c) \(y = \frac{{x - 3\sqrt {2 - x} }}{{\sqrt {x + 2} }}\)                     

d) \(y = \frac{{\sqrt {x - 1}  + \sqrt {4 - x} }}{{\left( {x - 2} \right)\left( {x - 3} \right)}}\)   

Cho hàm số 

\(f\left( x \right) = \left\{ \begin{array}{l}
 - 2\left( {x - 2} \right);\,\,\,\,\, - 1 \le x < 1\\
\sqrt {{x^2} - 1} ;\,\,\,\,\,\,\,\,\,\,\,x \ge 1
\end{array} \right.\)

a) Tìm tập xác định của hàm số

b) Tính \(f\left( { - 1} \right);f\left( {0,5} \right);f\left( {\frac{{\sqrt 2 }}{2}} \right);\)

\(f\left( 1 \right);f\left( 2 \right)\)

Trong các điểm A(- 2; 8); B(4;12), C(2;8) và \(D\left( {5;25 + \sqrt 2 } \right)\), điểm nào thuộc, điểm nào không thuộc đồ thị hàm số \(f\left( x \right) = {x^2} + \sqrt {x - 3} \)? Vì sao?

Khảo sát sự biến thiên của hàm số sau trên khoảng đã cho :

a) \(y = \frac{1}{{x - 2}}\) trên mỗi khoảng \(\left( { - \infty ;2} \right)\) và (2; + ∞ )

b) y = x² – 6x + 5 trên mỗi khoảng \(\left( { - \infty ;3} \right)\) và (3; + ∞)

c) y = x²⁰⁰⁵ + 1 trên khoảng (- ∞; + ∞ )

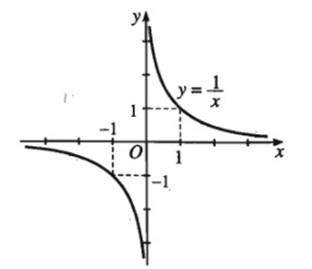
Hàm số \(y = \frac{1}{x}\) có đồ thị như hình 2.10

a) Dựa vào đồ thị, hãy lập bảng biến thiên của hàm số đó

b) Bằng tính toán, hãy khảo sát sự biến thiên của hàm số trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\) và kiểm tra lại kết quả so với bảng biến thiên đã lập

Tập con S của tập số thực R gọi là đối xứng nếu mọi x thuộc S, ta đều có – x thuộc S. Em có nhận xét gì về tập xác định của một hàm số chẵn (lẻ).

Từ nhận xét đó, em có kết luận gì về tính chẵn – lẻ của hàm số \(y = \sqrt x \)? Tại sao?

Gọi (d) là đường thẳng y = 2x và (d’) là đường thẳng y = 2x–3. Ta có thể coi (d’) có được là do tịnh tiến (d):

a) Lên trên hay xuống dưới bao nhiêu đơn vị?

b) Sang trái hay sang phải bao nhiêu đơn vị?

Cho đồ thị (H) của hàm số: \(y =  - \frac{2}{x}\)

a) Tịnh tiến (H) lên trên 1 đơn vị, ta được đồ thị của hàm số nào?

b) Tịnh tiến (H) sang trái 3 đơn vị, ta được đồ thị của hàm số nào?

c) Tịnh tiến (H) lên trên 1 đơn vị, sau đó tịnh tiến đồ thị nhận được sang trái 3 đơn vị, ta được đồ thị của hàm số nào ?

Tìm các cặp đường thẳng song song trong các đường thẳng sau:

a) \(y = \frac{1}{{\sqrt 2 }}x + 1\)

b) \(y =  - \frac{1}{{\sqrt 2 }}x + 3\)

c) \(y = \frac{2}{{\sqrt 2 }}x + 2\)

d) \(y = \sqrt 2 x - 2\)

e) \(y = \frac{1}{{\sqrt 2 }}x - 1\)

f) \(y =  - \left( {\frac{{\sqrt 2 }}{2}x - 1} \right)\)

Cho hàm số:

\(y = f\left( x \right) = \left\{ \begin{array}{l}
2x + 4,\,\,\,\, - 2 \le x <  - 1\\
 - 2x,\,\,\,\,\,\,\,\, - 1 \le x \le 1\\
x - 3,\,\,\,\,\,\,\,1 < x \le 3
\end{array} \right.\)

a) Tìm tập xác định và vẽ đồ thị của hàm số đó

b) Cho biết sự biến thiên của hàm số đã cho trên mỗi khoảng (- 2;- 1); (- 1;1) và (1;3) và lập bảng biến thiên của nó.

b) Cho phép tịnh tiến biến đồ thị hàm số \(f_1\) thành đồ thị hàm số \(f_2\)

Có phải mọi đường thẳng trong mặt phẳng toạ độ đều là đồ thị của một hàm số nào đó không ? Vì sao?

a) Tìm hàm số \(y = f(x)\), biết rằng đồ thị của nó là đường thẳng đi qua điểm (- 2;5) và có hệ số góc bằng -1,5 ;

b) Vẽ đồ thị của hàm số tìm được.

Tìm bốn hàm số bậc nhất của đồ thị là bốn đường thẳng đôi một cắt nhau tại bốn đỉnh của một hình vuông nhận gốc O làm tâm đối xứng, biết rằng một đỉnh của hình vuông này là A(3;0).

Gọi (G) là đồ thị của hàm số y = 2|x|

a) Khi tịnh tiến (G) lên trên 3 đơn vị, ta được đồ thị của hàm số nào ?

b) Khi tịnh tiến (G) sang trái 1 đơn vị, ta được đồ thị của hàm số nào ?

c) Khi tịnh tiến (G) sang phải 2 đơn vị, rồi xuống dưới 1 đơn vị, ta được đồ thị của hàm số nào?

Vẽ đồ thị của hai hàm số sau trên cùng một mặt phẳng tọa độ và nêu nhận xét về quan hệ giữa chúng:

a) y = |x – 2|

b) y = |x| - 3

Đi một hãng taxi quy định giá thuê xe đi mỗi kilômét là 6 nghìn đồng đối 10 km đầu tiên và 2,5 nghìn đồng đối với các kilômét tiếp theo. Một khách thuê taxi đi quãng đường x kilômét phải trả số tiền là y nghìn đồng. Khi đó, y là một hàm số của đối số x, xác định với mọi x ≥ 0.

a) Hãy biểu diễn y như một hàm số bậc nhất trên từng khoảng ứng với đoạn [0;10] và khoảng (10;+∞)

b) Tính \(f(8), f(10)\) và \(f(18)\).

c) Vẽ đồ thị của hàm số \(y = f(x)\) và lập bảng biến thiên cùa nó.

Cho hàm số: y = 3|x – 1| - |2x + 2|

a) Bằng cách bỏ dấu giá trị tuyệt đối, hãy viết hàm số đã cho dưới dạng hàm số bậc nhất trên từng khoảng.

(Hướng dẫn: Xét các khoảng hay đoạn \(\left( { - \infty ; - 1} \right),\left[ { - 1;1} \right)\) và \(\left[ {1; + \infty } \right)\)

b) Vẽ đồ thị rồi lập bảng biến thiên của hàm số đã cho.

Cho các hàm số 

a) \(y=-x^2-3\)

b) \(y=(x-3)^2\)

c) \(y = \sqrt 2 {x^2} + 1\)

d) \(y =  - \sqrt 2 {\left( {x + 1} \right)^2}\)

Không vẽ đồ thị, hãy mô tả đồ thị của mỗi hàm số trên bằng cách điền vào chỗ trống (...) theo mẫu:

- Đỉnh của parabol là điểm có tọa độ...

- Parabol có trục đối xứng là đường thẳng...

- Parabol hướng bề lõm (lên trên/ xuống dưới)...

Gọi (P) là đồ thị của hàm số y = ax² + c. Tìm a và c trong mỗi trường hợp sau:

a) y nhận giá trị bằng 3 khi x = 2 và có giá trị nhỏ nhất là - 1;

b) Đỉnh của parabol (P) là I(0; 3) và một trong hai giao điểm của (P) với trục hoành là A(- 2; 0).

Gọi (P) là đồ thị của hàm số y = a(x - m)². Tìm a và m trong mỗi trường hợp sau.

a) Parabol (P) có đỉnh là I(-3; 0) và cắt trục tung tại điểm M(0; -5);

b) Đường thẳng y = 4 cắt (P) tại hai điểm A(-1; 4) và B(3; 4).

Viết mỗi hàm số sau đây thành dạng \(y=a(x−p)^2+q\) từ đó hãy cho biết đồ thị của nó có thể suy ra từ đồ thị hàm số nào nhờ các phép tịnh tiến đồ thị song song với các trục tọa độ và mô tả cụ thể các phép tịnh tiến.
a) \(y=x^2-8x+12\)

b) \(y=-3x^2-12x+9\)

Hàm số \(y=−2x^2−4x+6\) có đồ thị là Parabol (P).

a) Tìm tọa độ đỉnh, phương trình trục đối xứng của (P).

b) Vẽ Parabol (P).

c) Dựa vào đồ thị, hãy cho biết tập hợp các giá trị của x sao cho y ≥ 0

Với mỗi hàm số \(y = -x^2 + 2x + 3\) và \(y = \frac{1}{2}{x^2} + x - 4\), hãy:   

a) Vẽ đồ thị của mỗi hàm số.

b) Tìm tập hợp các giá trị x sao cho y > 0.

c) Tìm tập hợp các giá trị x sao cho y < 0.

Lập bảng theo mẫu sau rồi điền vào ô trống các giá trị thích hợp (nếu có):

Gọi (P) là đồ thị hàm số tại y = ax² + bx + c. Hãy xác định dấu của hệ số a và biệt số Δ trong mỗi trường hợp sau:

a) (P) nằm hoàn toàn ở phía trên trục hoành

b) (P) nằm hoàn toàn ở phía dưới trục hoành

c) (P) cắt trục hoành tại hai điểm phân biệt và đỉnh của (P) nằm phía trên trục hoành

Vẽ đồ thị và lập bảng biến thiên của các hàm số sau:

a) \(y = \left| {{x^2} + \sqrt 2 x} \right|\)

b) \(y =  - {x^2} + 2\left| x \right| + 3\)

c) \(y = 0,5{x^2} - \left| {x - 1} \right| + 1\)

Vẽ đồ thị của mỗi hàm số sau:

a) \(y = \left\{ \begin{array}{l}
 - x + 1,\,\,\,\,\,\,x \le  - 1\\
 - {x^2} + 3,\,\,\,\,x >  - 1
\end{array} \right.\)

b) \(y = \left\{ \begin{array}{l}
\frac{1}{2}{\left( {x + 3} \right)^2},\,\,\,\,\,\,x \le  - 1\\
2,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x >  - 1
\end{array} \right.\)

Khi một quả bóng được đá lên sẽ đạt đến độ cao nhất, rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên; h là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá từ độ cao l,2m. Sau đó 1s, nó đạt được độ cao 8,5m, và 2s sau khi đá lên, nó ở độ cao 6m (hình dưới đây).

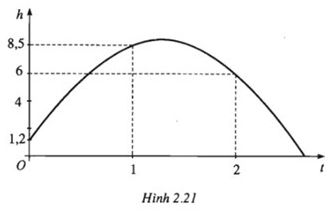
a) Hãy tìm: Hàm số có đồ thị trùng với quỹ đạo của bóng trong tình huống trên.

b) Sau bao lâu thì quả bóng sẽ chạm đất kể từ khi đá lên (chính xác đến hàng phần trăm).

c) Xác định độ cao lớn nhất của quả bóng (tính chính xác đến hàng phần nghìn)

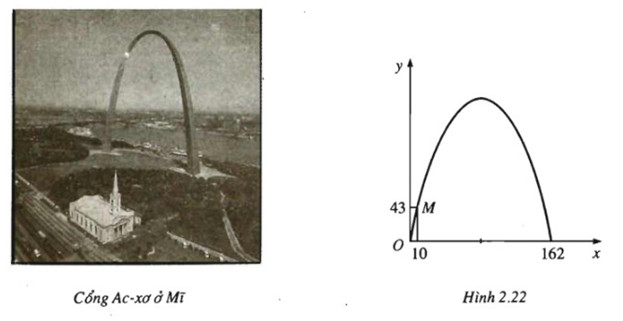
Bài toán về cổng Ac-xơ (Arch))

Khi du lịch đến thành phố Xanh lu-i (Mĩ) bạn sẽ thấy một cái cổng lớn hình parabol hướng bề lõm về phía dưới. Đó là cổng Ac-xơ. Giả sử lập một hệ tọa độ Oxy sao cho một chân cổng đi qua gốc O như hình vẽ dưới đây (x, y tính bằng mét), chân kia của cổng ở vị trí (162;0). Biết một điểm M trên cổng có tọa độ là (10;43).

a) Tìm hàm số có đồ thị là parabol nói trên (các hệ số chính xác đến hàng phần nghìn).

b) Tính chiều cao của công (Tính từ điểm cao nhất trên cổng xuống mặt đất, tính chính xác đến hàng đơn vị).

Với mỗi câu sau đây. Hãy chọn phần kết luận mà em cho là đúng:

a) Trên khoảng (-1; 1), hàm số y = - 2x + 5

(A) Đồng biến

(B) Nghịch biến;

(C) Cả kết luận (A) và (B) đều sai.

b) Trên khoảng (0; 1), hàm số y = x² + 2x - 3

(A) Đồng biến

(B) Nghịch biến;

(C) Cả kết luận (A) và (B) đều sai.

c) Trên khoảng (- 2; 1) hàm số y = x² + 2x - 3

(A) Đồng biến

(B) Nghịch biến;

(C) Cả kết luận (A) và (B) đều sai.

a) Tìm các hàm số lẻ trong các hàm số bậc nhất \(y=ax+b\)

b) Tìm các hàm số chẫn trong các hàm số bậc hai \(y=ax^2+bx+c\)

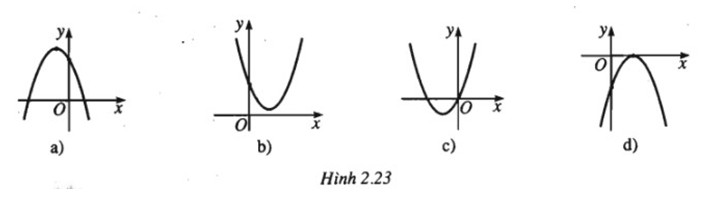
Dựa vào đồ thị của hàm số \(y=ax^2+bx+c\). Hãy xác định dấu của các hệ số a, b và c trong mỗi trường hợp dưới đây:

Trong mỗi trường hợp cho dưới đây, hãy vẽ đồ thị hàm số của các hàm số trên cùng một hệ trục tọa độ rồi xác định tọa độ giao điểm của chúng.

a) \(y=x-1\) và \(y=x^2-2x-1\)

b) \(y=-x+3\) và \(y=-x^2-4x+1\)

c) \(y=2x-5\) và \(y=x^2-4x-1\)

Xác định các hệ số a, b và c để cho hàm số \(y=ax^2+bx+c\) đạt giá trị nhỏ nhất bằng \(\frac{3}{4}\) khi \(x = \frac{1}{2}\) và nhận giá trị bằng 1 khi x = 1. Lập bảng biến thiên và vẽ đồ thị của hàm số.

Vẽ đồ thị của các hàm số sau rồi lập bảng biến thiên của nó

a) \(y = \left| {\frac{3}{2}x - 2} \right|\)

b) \(y = \left\{ \begin{array}{l}
2x,\,\,\,\,\,\,\,\,\,\,\,x < 0\\
{x^2} - x,\,\,\,\,x \ge 0
\end{array} \right.\)

c) \(y = \left| {\frac{1}{2}{x^2} + x - \frac{3}{2}} \right|\)

d) \(y = x\left| x \right| - 2x - 1\)

a) \(y = \left| {\frac{3}{2}x - 2} \right|\)

b) \(y = \left\{ \begin{array}{l}
2x,\,\,\,\,\,\,\,\,\,\,\,x < 0\\
{x^2} - x,\,\,\,\,x \ge 0
\end{array} \right.\)

c) \(y = \left| {\frac{1}{2}{x^2} + x - \frac{3}{2}} \right|\)

d) \(y = x\left| x \right| - 2x - 1\)

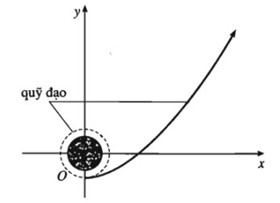
Khi một con tàu vũ trụ được phóng lên Mặt Trăng, trước hết nó sẽ bay vòng quanh Trái Đất. Sau đó, đến một thời điểm thích hợp, động cơ bắt đầu hoạt động đưa con tàu bay theo quỹ đạo là một nhánh hình parabol lên Mặt Trăng (trong hệ tọa độ Oxy như hình vẽ bên, X và y tính bằng nghìn kilômét). Biết rằng khi động cơ bắt đầu hoạt động, x = 0 thì y = - 7. Sau đó y = - 4 khi x = 10 và y = 5 khi x = 20.

a) Tìm hàm số có đồ thị là nhánh parabol nói trên.

b) Theo lịch trình, đế đến được Mặt Trăng, con tàu phải đi qua điểm (100;V) với \(y = 294 \pm 1,5\). Hỏi điều kiện đó có được thỏa màn hay không?

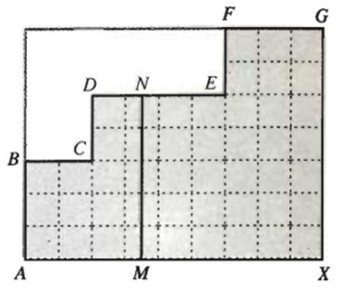
Trên hình bên, điểm M chuyển động trên đoạn thẳng AX. Từ M, kẻ đường thẳng song song với AB, cắt một trong ba đoạn thẳng BC, DE, FG tại điểm N. Gọi S là diện tích của miền tô đậm nằm ở bên trái MN. Gọi độ dài đoạn AM là x (0 < x < 9). Khi đó S là một hàm số của biến x. Hãy nêu biểu thức xác định hàm số S(x).