Bài tập 41 trang 63 SGK Toán 10 NC
Bài tập 41 trang 63 SGK Toán 10 NC
Dựa vào đồ thị của hàm số \(y=ax^2+bx+c\). Hãy xác định dấu của các hệ số a, b và c trong mỗi trường hợp dưới đây:
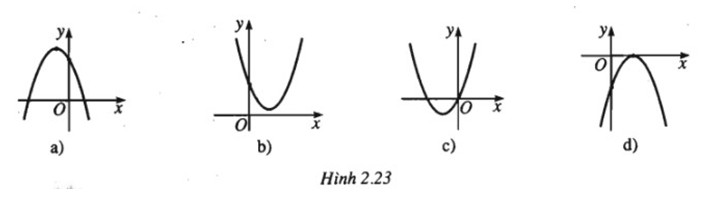
a) Parabol (P1) có bề lõm quay xuống nên \(a < 0\)
(P1) cắt trục Oy tại điểm có tung độ dương nên \(c = f(0) > 0\)
Hoành độ đỉnh \({x_0} = - \frac{b}{{2a}} < 0 \Rightarrow b < 0\) (do \(a < 0\))
b) Parabol (P2) có bề lõm quay lên nên \(a > 0\)
(P2) cắt trục Oy tại điểm có tung độ dương nên \(c = f(0) > 0\)
Hoành độ đỉnh \({x_0} = - \frac{b}{{2a}} > 0 \Rightarrow b < 0\) (do \(a >0\))
c) Parabol (P3) có bề lõm quay lên nên \(a > 0\)
(P3) đi qua gốc O nên \(c = 0\)
Hoành độ đỉnh \({x_0} = - \frac{b}{{2a}} < 0 \Rightarrow b > 0\) (do \(a >0\))
d) Parabol (P4) có bề lõm quay xuống nên \(a < 0\)
(P4) cắt trục Oy tại điểm có tung độ âm nên \(c < 0\)
Hoành độ đỉnh \({x_0} = - \frac{b}{{2a}} > 0 \Rightarrow b > 0\) (do \(a < 0\))
-- Mod Toán 10
Copyright © 2021 HOCTAP247
