Bài tập 9 trang 50 SGK Đại số 10

Bài tập 9 trang 50 SGK Đại số 10

Câu a:

Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y = \frac{1}{2}x - 1\)

Hàm số \(y = \frac{1}{2}x - 1\) có tập xác định là R.

Chiều biến thiên: Vì hàm số  \(y = \frac{1}{2}x - 1\)là hàm số bậc nhất có hệ số \(a = \frac{1}{2} > 0\) nên hàm số \(y = \frac{1}{2}x - 1\) đồng biến trên khoảng \(( - \infty ; + \infty ).\)

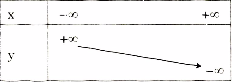
Bảng biến thiên khi x dần tới \( + \infty \) thì \(y = \frac{1}{2}x - 1\) dần tới \( + \infty \), khi x dần tới \( - \infty \) thì \( + \infty \) dần tới \( - \infty \). Ta có bảng biến thiên:

Đồ thị hàm số \(y = \frac{1}{2}x - 1\)

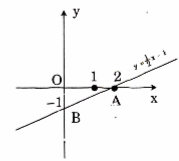
Vì đồ thị hàm số \(y = \frac{1}{2}x - 1\) là một đường thẳng nên ta chỉ việc xác định hai điểm phân biệt thuộc đồ thị, sau đó xác định đường thẳng qua hai điểm đó.

Cho \(x = 0 \Rightarrow y =  - 1\)

Cho \(y = 0 \Rightarrow x = 2\)

Vậy đường thẳng qua hai điểm A(2; 0), B(0; -1) chính là đồ thị của hàm số \(y = \frac{1}{2}x - 1\)

Câu b:

\(y = 4 - 2x\)

Tập xác định của hàm số \(y = 4 - 2x\)là \(\mathbb{R}\).

Chiều biến thiên. Vì hàm số đã cho là hàm số bậc nhất có hệ số a = -2 nên hàm số nghịch biến trên khoảng \(( - \infty ; + \infty )\)

Bảng biến thiên: Khi x dần tới \( + \infty \) thì y dần tới \( - \infty \), khi x dần tới \( - \infty \) thì y dần tới \( + \infty \). Ta có bảng biến thiên:

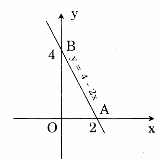
Đồ thị hàm số \(y = 4 - 2x\) là 1 đường thẳng đi qua hai điểm: A(2; 0); B(0; 4)

Đồ thị ở hình bên:

Câu c:

Hàm số \(y = \sqrt {{x^2}} \)có thể viết dưới dạng \(y = |x|\)

Tập xác định của hàm số \(y = |x|\) là tập \(\mathbb{R}\)

Chiều biến thiên:

Theo định nghĩa có giá trị tuyệt đối, ta có:

\(y = |x| = \left\{ \begin{array}{l}x\,\,\,\,\,\,neu\,\,x \ge 0\\ - x\,\,\,neu\,\,x < 0\end{array} \right.\)

Từ đó ta có: Hàm số\(y = |x|\)đồng biến trên khoảng \((0; + \infty )\) và nghịch biến trên khoảng \(( - \infty ; + 0)\)

Bảng biến thiên: khi x > 0 và x dần tới \( + \infty \) thì y = x dần tới \( + \infty \). Khi x < 0 và dần tới \( - \infty \) thì y = -x dần tới \( + \infty \). Ta có bảng biến sau đây:

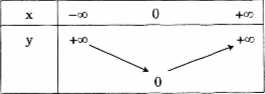
Đồ thị:

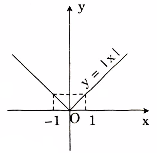
Trong nửa khoảng \({\rm{[}}0; + \infty )\) đồ thị của hàm số \(y = |x|\) trùng với đồ thị hàm số y = x (phần bên phải Oy)

Đồ thị có hình dạng sau:

Chú ý: Vì \(y = |x|\) là hàm số chẵn nên đồ thị của nó đối xứng qua trục tung.

Câu d:

Hàm số \(y = |x + 1|\)  có thể viết dưới dạng:

\(y = \left\{ \begin{array}{l}x + 1\,\,\,\,\,\,\,\,\,\,\,\,\,neu\,\,\,x \ge  - 1\\ - x - 1\,\,\,\,\,\,\,\,\,neu\,\,\,x <  - 1\end{array} \right.\,\,\,\,\,\,\,\,(*)\)

Tập xác định của hàm số \(y = |x + 1|\) là tập \(\mathbb{R}\)

Chiều biến thiên: Từ cách viết hàm số đã cho dưới dạng (*), ta có hàm số \(y = |x + 1|\) đồng biến trên khoảng \(( - 1; + \infty )\) và nghịch biến trên khoảng \(( - \infty ; - 1).\)

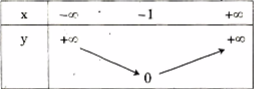
Bảng biến thiên: Khi x > - 1 và x dần tới \( + \infty \) thì y dần tới \( + \infty \).

Khi x < - 1 và x dần tới y = -x – 1 dần tới \( + \infty \). Ta có bảng biến thiên

Đồ thị

Trên nửa khoảng \({\rm{[}} - 1; + \infty )\) đồ thị của hàm số y = |x + 1| là đồ thị của hàm số y = x + 1.

Trên khoảng \(( - \infty ; - 1)\) đồ thị của hàm số y = |x + 1|là đồ thị của hàm số y = -x – 1.

-- Mod Toán 10