Bài tập 35 trang 60 SGK Toán 10 NC

Bài tập 35 trang 60 SGK Toán 10 NC

a) Vẽ đồ thị hàm số \(y = {x^2} + \sqrt 2 x\) (P₁) rồi suy ra đồ thị hàm số \(y = \left| {{x^2} + \sqrt 2 x} \right|\) (P)

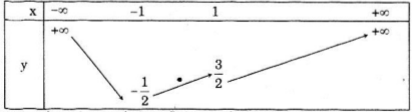
Hoành độ của đỉnh: 

\({x_0} =  - \frac{b}{{2a}} = \frac{{ - \sqrt 2 }}{2} \)

\(\Rightarrow {y_0} = \frac{1}{2} - 1 =  - \frac{1}{2}\)

Đỉnh \(I\left( {\frac{{ - \sqrt 2 }}{2}; - \frac{1}{2}} \right)\)

Bảng giá trị

Đồ thị hàm số

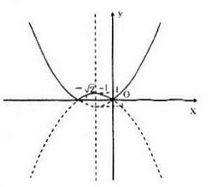
Ta giữ nguyên phần đồ thị trên trục hoành và lấy đối xứng phần đồ thì của hàm số \(y = {x^2} + \sqrt 2 x\) phía dưới trục hoành qua Ox ta được đồ thị của hàm \(y = \left| {{x^2} + \sqrt 2 x} \right|\) (đồ thị là phần nét liền trên hình vẽ)

Bảng biến thiên

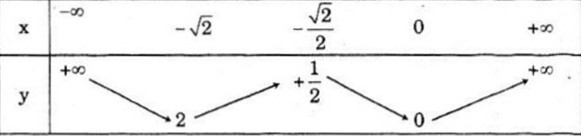
b) Vẽ đồ thị hàm số y = - x² + 2x + 3 (P₁) rồi suy ra đồ thị hàm số: y = - x² + 2|x| + 3 (P)

Hoành độ đỉnh: 

\({x_0} =  - \frac{b}{{2a}} = \frac{{ - 2}}{{ - 2}} = 1 \Rightarrow {y_0} = 4\)

Đỉnh I(1;4)

Bảng giá trị

Đồ thị hàm số

Bảng biến thiên

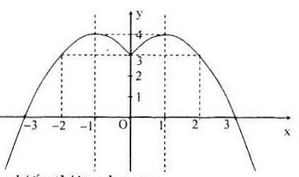
c) Ta có 

\(y = \left\{ {\begin{array}{*{20}{l}}
{0,5{x^2} - x + 2,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x \ge 1}\\
{0,5{x^2} + x,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x < 1}
\end{array}} \right.\)

Đồ thị hàm số

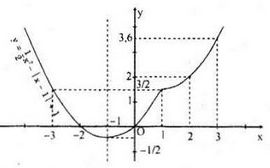
Bảng biến thiên

-- Mod Toán 10