Trang chủ
Lớp 10
Toán Lớp 10 SGK Cũ
Chương 2: Hàm Số Bậc Nhất Và Bậc Hai
Bài tập 5 trang 50 SGK Đại số 10
Bài tập 5 trang 50 SGK Đại số 10
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 5 trang 50 SGK Đại số 10
Chỉ ra khoảng đồng biến, khoảng nghịch biến của hàm số: \(y = {\rm{a}}{{\rm{x}}^2} + bx + c,\) trong mỗi trường hợp a > 0, a < 0.
Khi a > 0, hàm số \(y = {\rm{a}}{{\rm{x}}^2} + bx + c\) đồng biến trên khoảng \(\left( { - \frac{b}{{2a}}; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\)
Khi a < 0, hàm số \(y = {\rm{a}}{{\rm{x}}^2} + bx + c\) đồng biến trên khoảng \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\) và nghịch biến trên khoảng \(\left( { - \frac{b}{{2a}}; + \infty } \right)\)
Ta có bảng biến thiên của hàm số \(y = {\rm{a}}{{\rm{x}}^2} + bx + c\) cho hai trường hợp:

Trường hợp: a > 0
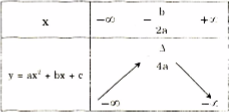
Trường hợp: a < 0
-- Mod Toán 10
Copyright © 2021 HOCTAP247
