Bài tập 43 trang 63 SGK Toán 10 NC
Bài tập 43 trang 63 SGK Toán 10 NC
Xác định các hệ số a, b và c để cho hàm số \(y=ax^2+bx+c\) đạt giá trị nhỏ nhất bằng \(\frac{3}{4}\) khi \(x = \frac{1}{2}\) và nhận giá trị bằng 1 khi x = 1. Lập bảng biến thiên và vẽ đồ thị của hàm số.
Đặt \(f(x)=ax^2+bx+c\)
Ta có
\(\left\{ \begin{array}{l}
{x_1} = - \frac{b}{{2a}}\\
f\left( {\frac{1}{2}} \right) = \frac{1}{4}a + \frac{1}{2}b + c\\
f\left( 1 \right) = a + b + c
\end{array} \right.\)
Tìm hệ số \(a, b, c\) thỏa hệ:
\(\begin{array}{l}
\left\{ {\begin{array}{*{20}{l}}
{ - \frac{b}{{2a}} = \frac{1}{2}}\\
{\frac{1}{4}a + \frac{1}{2}b + c = \frac{3}{4}}\\
{a + b + c = 1}
\end{array}} \right.\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a + b = 0}\\
{a + 2b + 4 = 3}\\
{a + b + c = 1}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a = 1}\\
{b = - 1}\\
{c = 1}
\end{array}} \right.
\end{array}\)
Vậy \(y=x^2-x+1\)
Bảng biến thiên
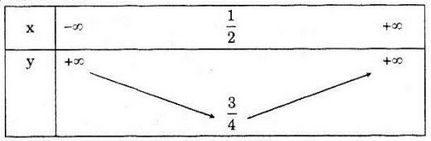
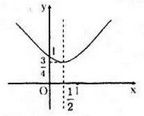
Đồ thị hàm số
-- Mod Toán 10
Copyright © 2021 HOCTAP247
