Bài tập 10 trang 51 SGK Đại số 10

Bài tập 10 trang 51 SGK Đại số 10

Câu a:

Hàm số \(y = {x^2} - 2x - 1\) có tập xác định là \(\mathbb{R}\)

Chiều biến thiên:

Vì hàm số \(y = {x^2} - 2x - 1\) có hệ số a =  1 > 0 nên ta có:

Hàm số đồng biến trên khoảng \((1; + \infty )\) và nghịch biến trên khoảng \(( - \infty ; - 1)\)

Bảng biến thiên:

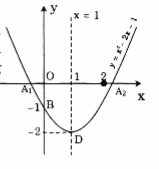
Đồ thị: Đồ thị của hàm số \(y = {x^2} - 2x - 1\) là một parabol có toạ độ đỉnh là D(1; -2) có trục đối xứng là đường thẳng x = 1

Giao của đồ thị với trục Oy là B(0; -1)

Đồ thị giao với Ox tại hai điểm: \({A_1}(1 - \sqrt 2 ;0);\,\,{A_2}(1 + \sqrt 2 ;0)\)

Đồ thị là hình vẽ bên:

Câu b:

 Hàm số \(y =  - {x^2} + 3x + 2\) có tập xác định là tập \(\mathbb{R}\)

Chiều biến thiên: Hàm số \(y =  - {x^2} + 3x + 2\)có hệ số a = -1< 0 nên ta có: Hàm số đồng biến trên khoảng \(( - \infty ;\frac{3}{2})\) và nghịch biến trên khoảng \((\frac{3}{2}; + \infty )\)

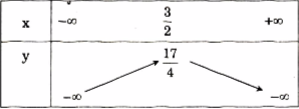
Bảng biến thiên: Khi x dần tới \( - \infty \) thì y dần tới \( - \infty \), khi x dần tới \( + \infty \) thì y dần tới \( - \infty \), khi \(x = \frac{3}{2}\) ta có \(y = \frac{{17}}{4}\), ta có bảng biến thiên

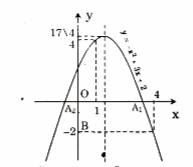
Đồ thị: Đồ thị hàm số \(y =  - {x^2} + 3x + 2\)là một parabol, toạ độ đỉnh là \(D = (\frac{3}{2};\frac{{17}}{4})\)  trục đối xứng là đường thẳng \(x = \frac{3}{2}\).

Đồ thị giao với Oy tại điểm B(0;2)

Đồ thị giao với Ox tại hai điểm:

\({A_1} = \left( {\frac{{3 + \sqrt {17} }}{2};0} \right);{A_2} = \left( {\frac{{3 - \sqrt {17} }}{2};0} \right)\)

-- Mod Toán 10