Bài tập 47 trang 75 SGK Hình học 11 NC

Bài tập 47 trang 75 SGK Hình học 11 NC

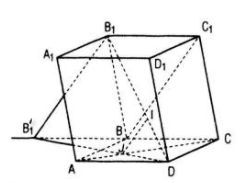
Giả sử, ta tìm được I ∈ B₁D, J ∈ AC sao cho  IJ // BC₁

Xét phép chiếu song song theo phương BC1 lên mp(ABCD). Khi đó hình chiếu của các điểm I , D, B₁ lần lượt là J, D , B₁’

Do D, I, B₁ thẳng hàng nên D, J, B₁’ thẳng hàng

Vậy J chính là giao điểm của hai đường thẳng B’₁D và AC. Từ đó ta có thể tìm I, J như sau:

- Dựng B’₁ là hình chiếu B₁ qua phép chiếu song song ở trên (BC₁B₁B’₁ là hình bình hành)

- Dựng J là giao điểm của B’₁D với AC

- Trong mp(B₁B’₁D) kẻ JI song song với B₁B’₁ cắt B₁D tại I

Rõ ràng I và J thỏa mãn điều kiện của bài toán

Dễ thấy B’₁ thuộc đường thẳng BC và \(AD = \frac{1}{2}B{'_1}C\)

Từ đó suy ra: 

\(\frac{{ID}}{{I{B_1}}} = \frac{{ID}}{{JB{'_1}}} = \frac{{AD}}{{B{'_1}C}} = \frac{1}{2}\)

Vậy ta có: \(\frac{{ID}}{{I{B_1}}} = \frac{1}{2}\)

-- Mod Toán 11