Trang chủ
Lớp 11
Toán Lớp 11 SGK Cũ
Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Bài tập 5 trang 53 SGK Hình học 11
Bài tập 5 trang 53 SGK Hình học 11
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 5 trang 53 SGK Hình học 11
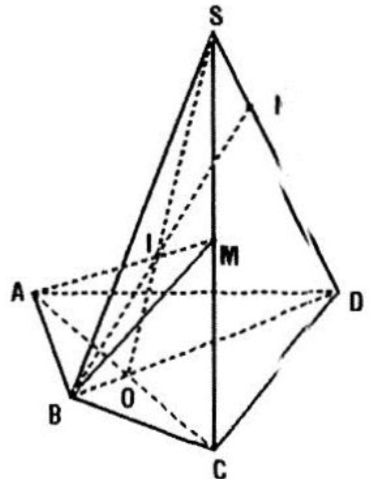
Cho tứ giác ABCD nằm trong mặt phẳng \((\alpha )\) có hai cạnh AB và CD không song song. Gọi S là điểm nằm ngoài mặt phẳng \((\alpha )\) và M là trung điểm đoạn SC.
a) Tìm giao điểm N của đường thẳng SD và mặt phẳng (MAB)
b) Gọi O là giao điểm của AC và BD. Chứng minh rằng ba đường thẳng SO, AM, BN đồng quy
Câu a:
Giao điểm N của SD với (MAB). Chọn mặt phẳng phụ (SBD) chứa SD. Gọi O là giao điểm của AC và BD và I là giao điểm của SO và AM thì \((SBD)\cap (ABM)=BI\). Gọi N là giao điểm của BI và SD (trên mặt phẳng (SBD)) thì N là giao điểm của SD và mp(MAB).
Câu b:
Theo câu a) ba đường thẳng SO, AM và BN đồng quy tại I.
-- Mod Toán 11
Copyright © 2021 HOCTAP247
