Bài tập 10 trang 54 SGK Hình học 11
Bài tập 10 trang 54 SGK Hình học 11
Cho hình chóp S. ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD
a) Tìm giao điểm N của đường thẳng CD và mặt phẳng (SBM)
b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)
c) Tìm giao điểm I của đường thẳng BM và mặt phẳng (SAC)
d) Tìm giao điểm P của SC và mặt pẳng (ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM)
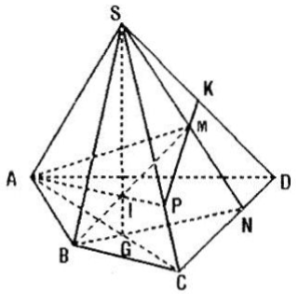
Câu a:
Trên mp(SCD) gọi N là giao điểm của SM và CD
⇒ N là giao điểm của CD và mp(SBM)
Câu b:
Gọi Q là giao điểm của BN và AC (trên mặt phẳng (ABCD))
⇒ S và Q là 2 điểm chung của 2 mặt phẳng (SBM) và (SAC).
\(\Rightarrow (SBM)\cap (SAC)=SQ\)
Câu c:
Gọi I là giao điểm của SQ và BM (trên mặt phẳng (SBM)).
Vì \(SQ\subset (SAC)\Rightarrow I\) là giao điểm của BM và mp(SAC)
Câu d:
Trên mặt phẳng (SAC) gọi P là giao điểm của AI và SC
Vì \(I\in BM, AI\subset (ABM)\Rightarrow P\) là giao điểm của SC và mp(ABM)
Trên mp(SCD) gọi K là giao điểm của SD và PM
Vì \(K\in PM\Rightarrow K\in (ABM)\)
⇒ 2 mặt phẳng (SCD) và (ABM) có 2 điểm chung P và K.
\(\Rightarrow (SCD)\cap (ABM)=PK\)
-- Mod Toán 11
Copyright © 2021 HOCTAP247
