Bài tập 4 trang 71 SGK Hình học 11
Bài tập 4 trang 71 SGK Hình học 11
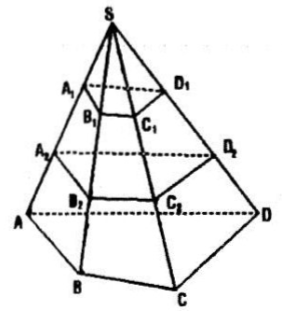
Cho hình chóp S.ABCD. Gọi \({A_{1}}^{}\) là trung điểm của cạnh SA và \({A_{2}}^{}\) là trung điểm của đoạn \(A{A_{1}}^{}\). Gọi \((\alpha )\) và \((\beta )\)là hai mặt phẳng song song với mặt phẳng (ABCD) và lần lượt đi qua \({A_{1}}^{}\), \({A_{2}}^{}\). Mặt phẳng \((\alpha )\) cắt các cạnh SB, SC, SD lần lượt tại \({B_{1}, {C_{1}, {D_{1}}^{}}^{}}^{}\). Mặt phẳng \((\beta )\) cắt các cạnh SB, SC, SD lần lượt tại \({B_{2}, {C_{2},{D_{2}}^{}}^{}}^{}\). Chứng minh:
a) \({B_{1}, {C_{1}, {D_{1}}^{}}^{}}^{}\) lần lượt là trung điểm của các cạnh SB, SC, SD
b) \({B_1}{B_2} = {B_2}B,\,\,{C_1}{C_2} = {C_2}C,\,\,{D_1}{D_2} = {D_2}D\)
c) Chỉ ra các hình chóp cụt có một đáy là tứ giác ABCD.
Câu a:
Vì mặt phẳng (SAB) cắt hai mặt phẳng song song \((\alpha )\) và (ABCD) theo hai giao tuyến lần lượt A1B1 và AB.
⇒ A1B1 // AB.
⇒ A1B1 là đường trung bình của tam giác SAB.
⇒ B1 là trung điểm của SB.
Tương tự ta có:
B1C1 là đường trung bình của tam giác SBC.
⇒ C1 là trung bình của SC.
C1D1 là đường trung bình của tam giác SCD.
⇒ D1 là trung điểm của SD.
Câu b:
Vì mp(SAB) cắt hai mặt phẳng song song \((\beta )\) và (ABCD) theo 2 giao tuyến lần lượt là A2B2 và AB.
⇒ A2B2 // AB
⇒ A2B2 là trung bình của hình thang A1B1BA
⇒ B1B2 = B2B
Tương tự: B2C2 là đường trung bình của hình thang B1C1CB
⇒ C1C2 = C2C
C2D2 là đường trung bình của hình thang C1D1DC
⇒ D1D2 = D2D
Câu c:
Có 2 hình chóp cụt có đáy là tứ giác ABCD đó là: A1B1C1D1.ABCD và A2B2C2D2.ABCD.
-- Mod Toán 11
Copyright © 2021 HOCTAP247
