Bài tập 2 trang 77 SGK Hình học 11
Bài tập 2 trang 77 SGK Hình học 11
Cho hình chóp S.ABCD là hình bình hành. Gọi M, N, P theo thứ tự là trung điểm của SA, BC, CD. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP). Gọi O là tâm hình bình hành, tìm giao điểm của đường thẳng SO với mặt phẳng (MNP).
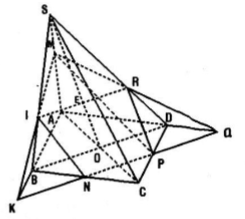
Trên mp(ABCD) gọi K là giao điểm của AB và NP. Trên mp(SAB), gọi I là giao điểm của MK và AB.
\( \Rightarrow \) M, K là 2 điểm chung của 2 mp(MNP) và (SAB)
\( \Rightarrow (MNP) \cap (SAB) = MI\)
Trên mp(ABCD) gọi Q là giao điểm của AD và NP. Trên mp (SAD) gọi R là giao điểm của MQ và SD.
\( \Rightarrow (MNP) \cap (SAD) = MR\) và \((MNP) \cap (ABCD) = NP\)
\( \Rightarrow \) Thiết diện của hình chóp khi cắt bởi mp(MNP) là ngũ giác MINPR.
Trên mp(SBD), gọi E là giao điểm của SO và IR.
Mà \({\rm{IR}} = (SBD) \cap (MNP) \Rightarrow E\) là giao điểm của SO và (MNP).
-- Mod Toán 11
Copyright © 2021 HOCTAP247
