Bài tập 8 trang 80 SGK Hình học 11 NC

Bài tập 8 trang 80 SGK Hình học 11 NC

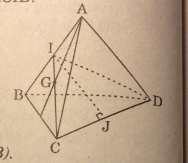
Gọi I là trung điểm của AB. Thiết diện cần tìm là ΔCID

Gọi J là trung điểm CD

ΔCID cân nên IJ ⊥ CD ⇒ \({S_{ICD}} = \frac{1}{2}IJ.CD\)

Ta có:

\(\begin{array}{l}
I{J^2} = C{I^2} - C{J^2} = {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} - \frac{{{a^2}}}{4} = \frac{{{a^2}}}{2}\\
 \Rightarrow IJ = \frac{{a\sqrt 2 }}{2} \Rightarrow {S_{ICD}} = \frac{1}{2}.\frac{{a\sqrt 2 }}{2}.a = \frac{{{a^2}\sqrt 2 }}{4}
\end{array}\)

Chọn (B).

-- Mod Toán 11