Bài tập 2 trang 63 SGK Hình học 11

Bài tập 2 trang 63 SGK Hình học 11

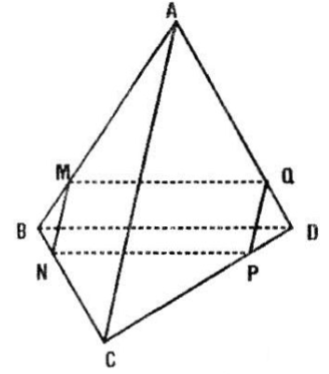
Câu a:

Ta có:

\((\alpha ) //AC\) và \(AC\subset (ABC)\)

⇒ AC song song với giao tuyến của \((\alpha )\) và (ABC)

* Trên mp(ABC) kẻ MN // AC \((N\in BC)\)

\(\Rightarrow MN=(\alpha )\cap (ABC)\)

\((\alpha ) // BD\) và \(BD\subset (ABC)\)

⇒ BD song song với giao tuyến của \((\alpha )\) và (BCD)

* Trên mp(BCD) kẻ \(NP // BD (P\in CD)\)

\(\Rightarrow NP=(\alpha )\cap (BCD)\)

\((\alpha ) //AC\) và \(AC\subset (ACD)\)

⇒ AC song song với giao tuyến của \((\alpha )\) và (ACD)

* Trên mp(ACD) kẻ PQ // AC \((Q\in AD)\)

\(\Rightarrow PQ=(\alpha )\cap (ACD)\)

Ta thấy M và Q là 2 điểm chung của mp\((\alpha )\) và (ABD)

\(\Rightarrow (\alpha )\cap (ABD)=MQ\)

Câu b:

Theo câu a) ta có:

\(\left.\begin{matrix} MN //AC\\ PQ //AC \end{matrix}\right\}\Rightarrow MN // PQ\)

và \((\alpha ) // BD, BD\subset (ABD)\Rightarrow BD // MQ\)

Mặt khác NP // AC ⇒ NP // MQ (2)

Từ (1) và (2) ⇒ MNPQ là hình bình hành 

⇒ Thiết diện cảu tứ diện cắt bởi mp\((\alpha )\) là hình bình hành.

-- Mod Toán 11