Trang chủ
Lớp 11
Toán Lớp 11 SGK Cũ
Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Bài tập 1 trang 59 SGK Hình học 11
Bài tập 1 trang 59 SGK Hình học 11
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 1 trang 59 SGK Hình học 11
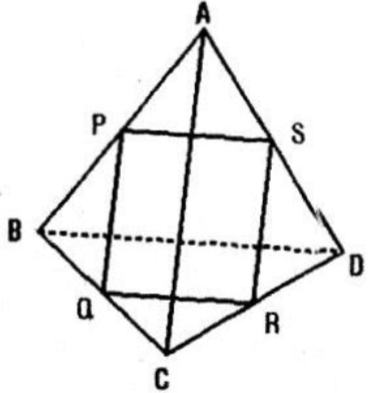
Cho tứ diện ABCD. Gọi P, Q, R, S là bốn điểm lần lượt lấy trên bốn cạnh AB, BC, CD, DA. Chứng minh rằng nếu bốn điểm P, Q, R, S đồng phẳng thì
a) Ba đường thẳng PQ, SR, AC hoặc song song hoặc đồng quy
b) Ba đường thẳng PS, RQ, BD hoặc song song hặc đồng quy
Câu a:
Ta có:
\(\begin{matrix} (PQRS)\cap (ABC)=PQ\\ (PQRS)\cap (ACD)=RS\\ (ABC) \cap (ACD)=AC \ \ \ \end{matrix}\)
Theo định lí về giao tuyến của 3 mp thì PQ, RS, AC hoặc đôi một cắt nhau hoặc đồng quy.
Câu b:
Chứng minh tương tự ta được ba đường thẳng PS, RQ, và BD hoặc song song hoặc đồng quy.
-- Mod Toán 11
Copyright © 2021 HOCTAP247
