Trang chủ
Lớp 11
Toán Lớp 11 SGK Cũ
Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Bài tập 1 trang 63 SGK Hình học 11
Bài tập 1 trang 63 SGK Hình học 11
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 1 trang 63 SGK Hình học 11
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.
a) Gọi O và O' lần lượt là tâm của các hình bình hành ABCD và ABEF. Chứng minh rằng đường thằng OO' song song với các mặt phẳng (ADF) và (BCF)
b) Gọi M và N lần lượt là trọng tâm của hai tam giác ABD và ABE. Chứng minh đường thẳng MN song song với mặt phẳng (CEF)
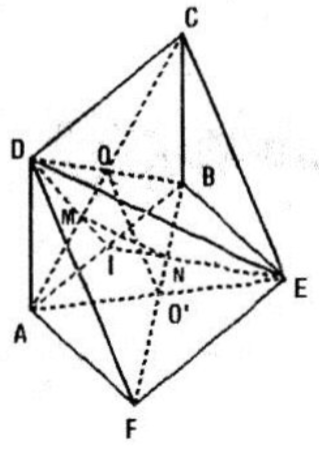
Câu a:
OO' là đường trung bình của \(\Delta DBF\) nên OO' // DF ⇒ OO' // (ADF)
Tương tự: OO' là đường trung bình của \(\Delta ACE\) ⇒ OO' // CE ⇒ OO' // (BCE)
Câu b:
Gọi I là trung điểm của AB thì DM và EN đều đi qua I và \(\frac{IM}{ID}=\frac{IN}{IE}\) (tính chất trọng tâm) ⇒ MN // DE mà DE nằm trong mp(CEF) và MN không nằm trong mp(CEF)
⇒ MM' // (CEF).
-- Mod Toán 11
Copyright © 2021 HOCTAP247
