Trang chủ
Lớp 11
Toán Lớp 11 SGK Cũ
Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Bài tập 7 trang 54 SGK Hình học 11
Bài tập 7 trang 54 SGK Hình học 11
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 7 trang 54 SGK Hình học 11
Cho bốn điểm A, B, C và D không đồng phẳng. Gọi I,K lần lượt là trung điểm của hai đoạn thẳng AD và BC
a) Tìm giao tuyến của hai mặt phẳng (IBC) và (KAD)
b) Gọi M và N là hai điểm lần lượt lấy trên hai đoạn thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng (IBC) và (DMN).
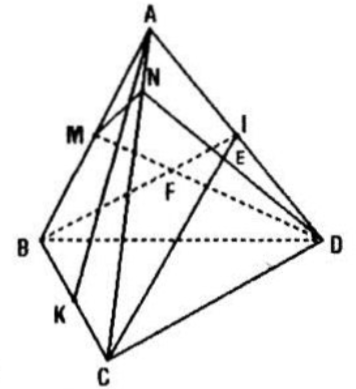
Câu a:
Ta có:
\(I\in AD\Rightarrow I\in (KAD)\Rightarrow I\) là điểm chung của 2 mặt phẳng (KAD) và (IBC).
\(K\in BC\Rightarrow K\in (IBC)\Rightarrow K\) là giao điểm chung của 2 mặt phẳng (KAD) và (IBC)
Vậy \((IBC)\cap (KAD)=IK\)
Câu b:
Trong mặt phẳng (ACD), gọi E là giao điểm của CI và DN.
Trong mặt phẳng (ABD), gọi F là giao điểm của BI và DM.
⇒ E, F là 2 điểm chung phân biệt của 2 mặt phẳng (IBC) và (DMN) nên \((IBC)\cap (DMN)= EF.\)
-- Mod Toán 11
Copyright © 2021 HOCTAP247
