Bài tập 7 trang 78 SGK Hình học 11 NC
Bài tập 7 trang 78 SGK Hình học 11 NC
Cho hình hộp ABCD.A’B’C’D’. Trên ba cạnh AB, DD’, C’B’ lần lượt lấy ba điểm M, N, P không trùng với các đỉnh sao cho \(\frac{{AM}}{{AB}} = \frac{{D\prime N}}{{D\prime D}} = \frac{{B\prime P}}{{B\prime C\prime }}\)
a. Chứng minh rằng mp(MNP) và mp(AB'D’) song song với nhau
b. Xác định thiết diện của hình hộp khi cắt bởi mp(MNP)
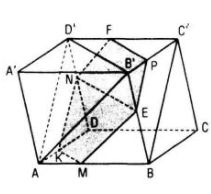
a) Kẻ ME song song với AB’ (E ∈ BB’) (1)
Ta có:
\(\frac{{B\prime E}}{{B\prime B}} = \frac{{AM}}{{AB}} \Rightarrow \frac{{B\prime E}}{{B\prime B}} = \frac{{B\prime P}}{{B\prime C\prime }}\)
⇒ EP // BC’ ⇒ EP // AD’ (2)
Từ (1) và (2) suy ra (MEP) // (AB’D’) (3)
Rõ ràng D’N = B’E nên EN // B’D’
Mà B’D’ ⊂ (AB’D’) và E ∈ (MEP) nên từ (3) suy ra EN ⊂ (MEP), tức (MNP) chính là (MEP)
Vậy (MNP) // (AB’D’)
b) Từ M kẻ ME song song với AB’, từ P kẻ PF song song với B’D’. Từ N kẻ NK song song với AD’ cắt AD tại K
Thiết diện là lục giác MEPFNK có các cạnh đối song song.
-- Mod Toán 11
Copyright © 2021 HOCTAP247
