Trang chủ
Lớp 11
Toán Lớp 11 SGK Cũ
Chương 1: Phép Dời Hình Và Phép Đồng Dạng Trong Mặt Phẳng
Bài tập 4 trang 34 SGK Hình học 11 NC
Bài tập 4 trang 34 SGK Hình học 11 NC
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 4 trang 34 SGK Hình học 11 NC
Cho vecto \({\vec u}\) và điểm O. Với điểm M bất kì, ta gọi M1là điểm đối xứng với M qua O và M’ là điểm sao cho \(\overrightarrow {{M_1}M} = \vec u\). Gọi F là phép biến hình biến M thành M’
a. F là phép hợp thành của hai phép nào ? F có phải là phép dời hình hay không ?
b. Chứng tỏ rằng F là một phép đối xứng tâm
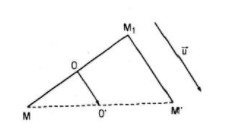
a) F là hợp thành của hai phép: phép đối xứng tâm ĐO với tâm O và phép tịnh tiến T theo vecto \({\vec u}\). Ta có F là phép dời hình vì ĐO và T là phép dời hình
b) Giả sử M1 = ĐO(M) và M’ = T(M1)
Nếu gọi O’ là trung điểm của MM’ thì:
\(\overrightarrow {OO'} = \frac{{\overrightarrow {{M_1}M'} }}{2} = \frac{{\overrightarrow u }}{2}\)
Vậy điểm O’ cố định và F chính là phép đối xứng qua tâm O’.
-- Mod Toán 11
Copyright © 2021 HOCTAP247
