Bài tập 4 trang 33 SGK Hình học 11

Bài tập 4 trang 33 SGK Hình học 11

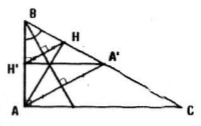
Cho tam giác ABC vuông cân tại A, AH là đường cao kẻ từ A. Tìm một phép đồng dạng biến tam giác HBA thành tam giác ABC.

Gọi d là đường phân giác của góc B, xét đối xứng trục Đd ta đó: A' = Đ_d(A) ⇒ A' là giao điểm của đường thẳng đi qua A với cạnh BC, H' = Đ_d(H) ⇒ H' là giao điểm của đường thẳng đi qua H với AB.

B = Đ_d(B), vậy \(\Delta H'BA'\) là ảnh của \(\Delta HBA\) qua phép đối xứng trục Đ_d.

Ta có \(\Delta HBA, \Delta ABC\) nên \(\Delta H'BA' \sim \Delta ABC\) do đó: 

\(\frac{AB}{H'B}=\frac{AC}{H'A'}=\frac{AC}{AH}\)

Xét phép vị tự \(V_{\left ( B, \frac{AC}{AH} \right )}\), ta có:

\(A=V_{\left ( B, \frac{AC}{AH} \right )}, (H'),C=V_{\left ( B, \frac{AC}{AH} \right )} (A'), B=V_{\left ( B, \frac{AC}{AH} \right )}(B)\)

Hay \(\Delta ABC\) là ảnh của \(\Delta HBA\) qua phép đồng dạng thu được từ việc thực hiện liên tiếp phép đối xứng qua đường phân giác của góc B và phép vị tự tâm B, tỉ số \(\frac{AC}{AH}.\)

-- Mod Toán 11