Bài tập 2 trang 24 SGK Hình học 11
Bài tập 2 trang 24 SGK Hình học 11
Cho hình chữ nhật ABCD. Gọi E, F, H, K, O, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, DA, KF, HC, KO. Chứng minh hai hình thang AEJK và FOIC bằng nhau.
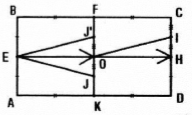
Xét phép đối xứng trục ĐEH ta có:
F = ĐEH (K), B = ĐEH (B), E = ĐEH(E), ĐEH (J) = J' (J' là trung điểm OF).
Vậy ảnh của hình thang AEJK qua ĐEH là hình thang BEJ'F (1).
Xét phép tịnh tiến \({T_{\overrightarrow {EO} }}\) ta có \(F = {T_{\overrightarrow {EO} }}(B),\,I = {T_{\overrightarrow {EO} }}(J'),\,C = {T_{\overrightarrow {EO} }}(F),O = {T_{\overrightarrow {EO} }}(E).\)
Vậy hình thang FOIC là ảnh của hình thang BEJ'F qua \({T_{\overrightarrow {EO} }}\) (2).
Từ (1) và (2) ta có tồn tại phép dời hình (thực hiện liên tiếp hai phép dời hình là đối xứng trục và tịnh tiến ta cũng được một phép dời hình) biến hình thang AEJK thành hình thang FOIC hay hai hình thang đó bằng nhau.
-- Mod Toán 11
Copyright © 2021 HOCTAP247
